53 Chinese Remainder Theorem

We now return to a basic result of number theory that will be used later.

Let n₁,n₂,…,n_k be positive pairwise relatively prime positive integers¹ , let n = ∏ _i=1^kn_i, and let a_i Z_i for i = 1,…,k. Consider the system of congruence equations with unknown x:

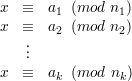(1)

The Chinese Remainder Theorem says that (1) has a unique solution in Z_n.

To solve for x, let

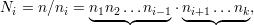
and compute M_i = N_i^-1 mod n_i, for 1 ≤ i ≤ k. Note that N_i^-1 (mod n_i) exists since gcd(N_i,n_i) = 1 by the pairwise relatively prime condition. We can compute N_i^-1 using the methods of section 47 (lecture notes 11). Now let

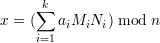(2)

If j≠i, then M_jN_j ≡ 0 (mod n_i) since n_i|N_j. On the other hand, M_iN_i ≡ 1 (mod n_i) by definition of M_i. Hence,

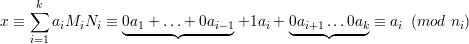(3)

for all 1 ≤ i ≤ k, establishing that (2) is a solution of (1).

To see that the solution is unique in Z_n, let χ be the mapping x(x mod n₁,…,x mod n_k). χ is a surjection² from Z_n to Z_n1 ×…× Z_nk since we have just shown for all (a₁,…,a_k) Z_n1 ×…× Z_nk that there exists x Z_n such that χ(x) = (a₁,…,a_k). Since also |Z_n| = |Z_n1 ×…×Z_nk|, χ is a bijection, and (1) has only one solution in Z_n.

A less slick but more direct way of seeing the same thing is to suppose that x = u and x = v are both solutions to (1). Then u ≡ v (mod n_i), so n_i|(u - v) for all i. By the pairwise relatively prime condition on the n_i, it follows that n|(u - v), so u ≡ v (mod n). Hence, the solution is unique in Z_n.

54 Homomorphic property of χ

The bijection χ is interesting in its own right, for it establishes a one-to-one correspondence between members of Z_n and k-tuples (a₁,…,a_k) in Z_n1 ×… × Z_nk. This lets us reason about and compute with k-tuples and then translate the results back to Z_n.

The homomorphic property of χ means that performing an arithmetic operation on x Z_n corresponds to performing the similar operation on each of the components of χ(x). More precisely, let ⊙ be one of the arithmetic operations +, -, or ×. If χ(x) = (a₁,…,a_k) and χ(y) = (b₁,…,b_k), then

(4)

In other words, if one first performs z = (x ⊙ y) mod n and then computes z mod n_i, the result is the same as if one instead first computed a_i = (x mod n_i) and b_i = (y mod n_i) and then performed (a_i ⊙ b_i) mod n_i. This relies on the fact that (z mod n) mod n_i = z mod n_i, which holds because n_i ∣ n.

55 RSA Decryption Works for All of Z_n

In section 44 (lecture notes 10), we showed that RSA decryption works when m,c Z*_n but omitted the proof that it actually works for all m,c Z_n. We now use the Chinese Remainder Theorem to supply this missing piece.

Let n = pq be an RSA modulus, p,q distinct primes, and let e and d be the RSA encryption and decryption exponents, respectively. We show m^ed ≡ m (mod n) for all m Z_n.

Define a = (m mod p) and b = (m mod q), so

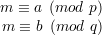(5)

Raising both sides to the power ed gives

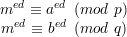(6)

We now argue that a^ed ≡ a (mod p). If a ≡ 0 (mod p), then obviously a^ed ≡ 0 ≡ a (mod p). If a ⁄≡ 0 (mod p), then gcd(a,p) = 1 since p is prime, so a Z*_p. By Euler’s theorem,

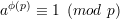
Since ed ≡ 1 (mod ϕ(n)), we have ed = 1 + uϕ(n) = 1 + uϕ(p)ϕ(q) for some integer u. Hence,

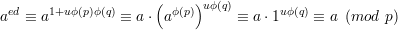(7)

Similarly,

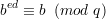(8)

Combining the pair (6) with (7) and (8) yields

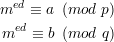
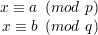(9)

From (5), m is also a solution of (9). By the Chinese Remainder Theorem, the solution to (9) is unique modulo n, so m^ed ≡ m (mod n) as desired.

56 RSA Security

Several possible attacks on RSA are discussed below and their relative computational difficulties discussed.

56.1 Factoring n

The security of RSA depends on the computational difficulty of several different problems, corresponding to different ways that Eve might attempt to break the system. The first of these is the RSA factoring problem: Given a number n that is known to be the product of two primes p and q, find p and q. Clearly if Eve can find p and q, then she can compute the decryption key d from the public encryption key e (in the same way that Alice did when generating the key) and subsequently decrypt all ciphertexts.

56.2 Computing ϕ(n)

Eve doesn’t really need to know the factors of n in order to compute d. It is enough for her to know ϕ(n). Computing ϕ(n) is no harder than factoring n since ϕ(n) is easily computed given the factors of n, but is it perhaps easier? If it were, then Eve would have a possible attack on RSA different from factoring n. It turns out that it is not easier, for if Even knows ϕ(n), then she can factor n. She simply sets up the system of quadratic equations

56.3 Finding d

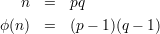
Another possibility is that Eve might somehow be able to compute d from e and n even without the ability to factor n or compute ϕ(n). That would represent yet another attack that couldn’t be ruled out by the assumption that the RSA factoring problem is hard. However, that too is not possible, as we now show.

Suppose Eve knows n and e and is somehow able to obtain d. Then Eve can factor n by a probabilistic algorithm. The algorithm is presented in Figure56.1.

To factor n: /* Find s, t such that ed - 1 = 2st and t is odd */ s = 0; t = ed - 1; while (t is even ) {s++; t∕=2;} /* Search for non-trivial square root of 1 (mod n) */ do { /* Find a random square root b of 1 (mod n) */ choose a Z*n at random; b = at mod n; while (b2 ⁄≡ 1 (mod n)) b = b2 mod n; } while (b ≡±1 (mod n)); /* Factor n */ p = gcd(b - 1,n); q = n∕p; return (p,q); } Figure 56.1: Algorithm for factoring n given d.

We begin by finding unique integers s and t such that 2^st = ed- 1 and t is odd. This is always possible since ed - 1≠0. One way to find s and t is to express ed - 1 in binary. Then s is the number of trailing zeros and t is the value of the binary number that remains after the trailing zeros are removed. Since ed - 1 ≡ 0 (mod ϕ(n)) and 4∣ϕ(n) (since both p - 1 and q - 1 are even), it follows that s ≥ 2.

Now, for each a chosen at random from Z*_n, define a sequence b₀,b₁,…,b_s, where b_i = a^2it mod n, 0 ≤ i ≤ s. Each number in the sequence is the square of the number preceding it modulo n. The last number in the sequence is 1 by Euler’s theorem and the fact that ϕ(n)∣(ed- 1). Since 1² mod n = 1, every element of the sequence following the first 1 is also 1. Hence, the sequence consists of a (possibly empty) block of non-1 elements, following by a block of 1’s.

It is easily verified that b₀ is the value of b when the innermost while loop is first entered, and b_k is the value of b after the k^th iteration of that loop. The loop executes at most s- 1 times since it terminates just before the first 1 is encounter, that is, when b² ≡ 1 (mod n). At this time, b = b_k is a square root of 1 (mod n).

Over the reals, we know that each positive number has two square roots, one positive and one negative, and no negative numbers have real square roots. Over Z*_n for n = pq, it turns out that 1∕4 of the numbers have square roots, and each number that has a square root actually has four. Since 1 does have a square root modulo n (itself), there are four possibilities for b: ±1 mod n and ±r mod n for some r Z*_n, r ⁄≡±1 (mod n).

The do loop terminates if and only if b ⁄≡±1 (mod n). At that point we can factor n. Since b² ≡ 1 (mod n), we have n∣(b² - 1) = (b + 1)(b- 1). But since b ⁄≡±1 (mod n), n does not divide b + 1 and n does not divide b - 1. Therefore, one of the factors of n divides b + 1 and the other divides b - 1. Hence, gcd(b - 1,n) is a non-trivial factor of n.

It can be shown that there is at least a 0.5 probability that b ⁄≡±1 (mod n) for the b computed by this algorithm in response to a randomly chosen a Z*_n. Hence, the expected number of iterations of the do loop is at most 2. (See Evangelos Kranakis, Primality and Cryptography, Theorem 5.1 for details.)

Here’s a simple example of the use of this algorithm. Suppose n = 5 × 11 = 55, e = 3, and d = 27. (These are possible RSA values since ϕ(n) = 40 and ed = 81 ≡ 1 (mod 40).) Then ed - 1 = 80 = (1010000)₂, so s = 4 and t = 5.

Now, suppose we take a = 2. We compute the sequence of b’s as follows:

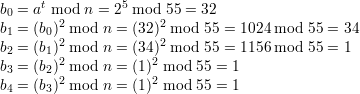
Since the last b_i≠1 in this sequence is 34, and 34 ⁄≡-1 (mod 55), then 34 is a non-trivial square root of 1 modulo 55. It follows that gcd(34 - 1,55) = 11 is a prime divisor of n.

56.4 Finding plaintext

Eve isn’t really interested in factoring n, computing ϕ(n), or finding d, except as a means to read Alice’s secret messages. Hence, the problem we would like to be hard is the problem of computing the plaintext m given an RSA public key (n,e) and a ciphertext c. The above shows that this problem is no harder than factoring n, computing ϕ(n), or finding d, but it does not rule out the possibility of some clever way of decrypting messages without actually finding the decryption key. Perhaps there is some feasible probabilistic algorithm that finds m with non-negligible probability, maybe not even for all ciphertexts c but for some non-negligible fraction of them. Such a method would “break” RSA and render it useless in practice. No such algorithm has been found, but neither has the possibility been ruled out, even under the assumption that the factoring problem itself is hard.

57 Primitive Roots

We have completed our discussion of RSA. We turn next to other number-theoretic techniques with important cryptographic applications. We begin by looking in greater detail at the structure of Z*_n, the set of integers relatively prime to n.

Let g Z*_n and consider the successive powers g,g²,g³,…, all taken modulo n. Because Z*_n is finite, this sequence must eventually repeat. By Euler’s theorem, this sequence contains 1 since g^k = 1 (in Z_n) for k = ϕ(n). Let k be the smallest positive integer such that g^k = 1. We call k the order of g and write ord(g) = k. The elements {g,g²,…,g^k = 1} form a subgroup S of Z*_n. The order of S (number of elements in S) is ord(g); hence ord(g)∣ϕ(n). We say that g generates S and that S is cyclic.

We say g is a primitive root of n if g generates all of Z*_n, that is, every element of Z*_n can be written as g raised to some power modulo n. By definition, this holds if and only if ord(g) = ϕ(n). Not every integer n has primitive roots. By Gauss’s theorem, the numbers having primitive roots are 1,2,4,p^k,2p^k, where p is an odd prime and k ≥ 1. In particular, every prime has primitive roots.

The number of primitive roots of p is ϕ(ϕ(p)). This is because if g is a primitive root of p and x Z*_ϕ(p), then g^x is also a primitive root of p. Why? We need to argue that every element h in Z*_p can be expressed as (g^x)^y for some y. Since g is a primitive root, we know that h ≡ g^ℓ (mod p) for some ℓ. We wish to find y such that g^xy ≡ g^ℓ (mod n). By Euler’s theorem, this is possible if the congruence equation xy ≡ ℓ (mod ϕ(n)) has a solution y. We know that a solution exists if gcd(x,ϕ(n)) = 1. But this is the case since x was chosen to be in Z*_ϕ(p).