57 Primitive Roots (continued)

Lucas test: g is a primitive root of p if and only if

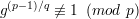
for all q > 1 such that q∣(p - 1).

Clearly if the test fails for some q, then ord(g) ≤ (p- 1)∕q < p- 1 = ϕ(p), so g is not a primitive root of p. Conversely, if ord(g) < ϕ(p), then the test will fail for q = (p - 1)∕ord(g), which is one of the q’s included in the test since ord(g)∣ϕ(p).

A drawback to the Lucas test is that one must try all the divisors of p - 1, and there can be many. Moreover, to find the divisors efficiently implies the ability to factor. Thus, it does not lead to an efficient algorithm for finding a primitive root of an arbitrary prime p. However, there are some special cases which we can handle.

Let p and q be odd primes such that p = 2q + 1. There are lots of examples of such pairs, e.g., q = 41 and p = 83. In this case, p - 1 = 2q, so p - 1 is easily factored and the Lucas test easily employed. How many primitive roots of p are there? From the above, the number is ϕ(ϕ(p)) = ϕ(p - 1) = ϕ(2)ϕ(q) = q - 1. Hence, the density of primitive roots in Z* _p is (q - 1)∕(p - 1) = (q - 1)∕2q ≈ 1∕2. This makes it easy to find primitive roots of p probabilistically — choose a random element a Z*_p and apply the Lucas test to it.

We defer the question of the density of primes q such that 2q + 1 is also prime but remark that we can relax the requirements a bit. Suppose we start with a prime q and then consider the numbers 2q + 1,3q + 1,4q + 1,… until we find a prime p = uq + 1 in this sequence. By the prime number theorem, approximately one out of every ln(q) numbers around the size of q will be prime. While that applies to randomly chosen numbers, not the numbers in this particular sequence, there is at least some hope that the density of primes will be similar. If so, we can expect that u will be about ln(q), in which case it can be easily factored using exhaustive search. At that point, we can apply the Lucas test as before to find primitive roots.

58 Discrete Logarithm

Let y = b^x over the reals. The ordinary base-b logarithm is the inverse of the exponential function, so log _b(y) = x. The discrete logarithm is defined similarly, but now arithmetic is performed in Z*_p for a prime p. In particular, the discrete log to the base b of y modulo p is defined to be the least non-negative integer x such that y ≡ b^x (mod p) (if it exists), and we write x = log _b(y) mod p. If b is a primitive root of p, then log _b(y) is defined for every y Z*_p.

The discrete log problem is the problem of computing log _b(y) mod p given a prime p and primitive root b of p. No known efficient algorithm is known for this problem and it is believed to be intractable. However, it’s inverse, the function power_b(x) = b^x mod p, is easily computable, so power_b is an example of a so-called one-way function, that is a function that is easy to compute but hard to invert.

59 Diffie-Hellman Key Exchange

Alice    Bob    Choose random x Zϕ(p).   Choose random y Zϕ(p). a = gx mod p.    b = gy mod p. Send a to Bob.    Send b to Alice.     ka = bx mod p.    kb = ay mod p. Figure 59.1: Diffie-Hellman Key Exchange Protocol.

The key exchange problem is for Alice and Bob to agree on a common random key k. One way for this to happen is for Alice to choose k at random and then communicate it to Bob over a secure channel. But that presupposes the existence of a secure channel. The Diffie-Hellman Key Exchange protocol allows Alice and Bob to agree on a secret k without having prior secret information and without giving an eavesdropper Eve any information about k. The protocol is given in Figure 59.1. We assume that p and g are publicly known, where p is a large prime and g a primitive root of p. Clearly, k_a = k_b since k_a ≡ b^x ≡ g^xy ≡ a^y ≡ k_b (mod p). Hence, k = k_a = k_b is a common key. In practice, Alice and Bob can use this protocol to generate a session key for a symmetric cryptosystem, which then can subsequently use to exchange private information.

The security of this protocol relies on Eve’s presumed inability to compute k from a and b and the public information p and g. This is sometime called the Diffie-Hellman problem and, like discrete log, is believed to be intractable. Certainly the Diffie-Hellman problem is no harder that discrete log, for if Eve could find the discrete log of a, then she would know x and could compute k_a the same way that Alice does. However, it is not known to be as hard as discrete log.

60 ElGamal Key Agreement

A variant of the above algorithm has Bob going first followed by Alice, as shown in Figure 60.1.

Alice    Bob       Choose random y Zϕ(p).    b = gy mod p.    Send b to Alice.     Choose random x Zϕ(p).   a = gx mod p.    Send a to Bob.        ka = bx mod p.    kb = ay mod p.    Figure 60.1: ElGamal Variant of Diffie-Hellman Key Exchange.

The difference here is that Bob completes his action at the beginning and no longer has to communicate with Alice. Alice, at a later time, can complete her half of the protocol and send a to Bob, at which point Alice and Bob share a key.

This is just the scenario we want for public key cryptography. Bob generates a public key (p,g,b) and a private key (p,g,y). Alice (or anyone who obtains Bob’s public key) can complete the protocol by sending a to Bob. This is the idea behind the ElGamal public key cryptosystem.

Assume Alice knows Bob’s public key (p,g,b). To encrypt a message m, she first completes her part of the protocol of Figure 60.1 to obtain numbers a and k. She then computes c = mk mod p and sends the pair (a,c) to Bob. When Bob gets this message, he first uses a to complete his part of the protocol and obtain k. He then computes m = k^-1c mod p.

While the ElGamal cryptosystem uses the simple encryption function E_k(m) = mk mod p to actually encode the message, it should be clear that any symmetric cryptosystem could be used at that stage. An advantage of using a standard system such as AES is that long messages can be sent following only a single key exchange.

Putting this all together gives us the following variant of the ElGamal public key cryptosystem. As before, Bob generates a public key (p,g,b) and a private key (p,g,y). To encrypt a message m to Bob, Alice first obtains Bob’s public key and chooses a random x Z_ϕ(p). She next computes a = g^x mod p and k = b^x mod p. She then computes

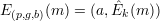
and sends it to Bob. Here, Ê is the encryption function of a specified symmetric cryptosystem. Bob receives a pair (a,c). To decrypt, Bob computes k = a^y mod p and the computes m = 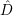_k(c).

We remark that a new element has been snuck in here. The ElGamal cryptosystem and its variants require Alice to generate a random number which is then used in the course of encryption. Thus, the resulting encryption function is a random function rather than an ordinary function. A random function is one that can return different values each time it is called, even for the same arguments. The way to view a random function is that it specifies a probability distribution on the output space that depends on its arguments.

In the case of E_(p,g,b)(m) each message m has many different possible encryptions. An advantage of such a probabilistic encryption system is that Eve can no longer use the public encryption function to check a possible decryption, for even if she knows m, she cannot verify m is the correct decryption of (a,c) simply by computing E_(p,g,b)(m) as she could do for a deterministic cryptosystem such as RSA. Two disadvantages of course are that Alice must have a source of randomness in order to use the system, and the ciphertext is longer than the corresponding plaintext.