61 Quadratic Residues, Squares, and Square Roots

An integer a is called a quadratic residue (or perfect square) modulo n if a ≡ b² (mod n) for some integer b. Such a b is said to be a square root of a modulo n. We let

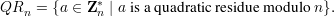
be the set of quadratic residues in Z*_n, and we denote the set of non-quadratic residues in Z*_n by QNR_n = Z*_n - QR_n.

62 Square Roots Modulo a Prime

For example, take p = 11. The following table shows all of the elements of Z*₁₁ and their squares.

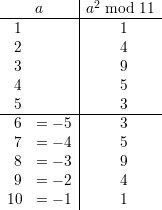
Thus, we see that QR₁₁ = {1,3,4,5,9} and QNR₁₁ = {2,6,7,8,10}.

Proof: We now prove Claim 1. Consider the mapping sq : Z*_p → QR_p defined by bb² mod p. We show that this is a 2-to-1 mapping from Z*_p onto QR_p.

Let a QR_p, and let b² ≡ a (mod p) be a square root of a. Then -b is also a square root of a, and b ⁄≡-b (mod p) since p ~ ∣ 2b. Hence, a has at least two distinct square roots (mod n). Now let c be any square root of a.

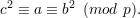
Then p∣c² - b², so p∣(c - b)(c + b). Since p is prime, then either p∣(c - b), in which case c ≡ b (mod p), or p∣(c + b), in which case c ≡ -b (mod p). Hence c ≡ ±b (mod p). Since c was an arbitrary square root of a, it follows that ±b are the only two square roots of a. Hence, sq() is a 2-to-1 function, and |QR_p| = 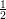|Z*_p| as desired. __

63 Square Roots Modulo the Product of Two Primes

Proof: Consider the mapping sq : Z*_n → QR_n defined by bb² mod n. We show that this is a 4-to-1 mapping from Z*_n onto QR_n.

Let a QR_n and let b² ≡ a (mod n) be a square root of a. Then also b² ≡ a (mod p) and b² ≡ a (mod q), so b is a square root of a (mod p) and b is a square root of a (mod q). Conversely, if b_p is a square root of a (mod p) and b_q is a square root of a (mod q), then by the Chinese Remainder theorem, the unique number b Z*_n such that b ≡ b_p (mod p) and b ≡ b_q (mod q) is a square root of a (mod n). Since a has two square roots mod p and two square roots mod q, it follows that a has four square roots mod n. Thus, sq() is a 4-to-1 function, and |QR_n| = 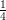|Z*_n| as desired. __

64 Euler Criterion

There is a simple test due to Euler for whether a number is in QR_p for p prime.

Claim 3 (Euler Criterion): An integer a is a non-trivial¹ quadratic residue modulo p iff

Proof: Let a ≡ b² (mod p) for some b ⁄≡ 0 (mod p). Then

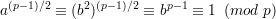
by Euler’s theorem, as desired.

For the other direction, suppose a^(p-1)∕2 ≡ 1 (mod p). Clearly a ⁄≡ 0 (mod p). We show that a is a quadratic residue by finding a square root b modulo p.

Let g be a primitive root of p. Choose k so that a ≡ g^k (mod p), and let ℓ = (p - 1)k∕2. Then

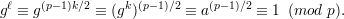
Because g is a primitive root, g^ℓ ≡ 1 (mod p) implies that ℓ is a multiple of p - 1. Hence, (p - 1)∣(p - 1)k∕2, from which we conclude that 2|k and k∕2 is an integer. Let b = g^k∕2. Then b² ≡ g^k ≡ a (mod p), so b is a square root of a modulo p, as desired. __

65 Finding Square Roots Modulo Special Primes

The Euler criterion lets us test membership in QR_p for prime p, but it doesn’t tell us how to find square roots. In case p ≡ 3 (mod 4), there is an easy algorithm for finding the square roots of any member of QR_p.

Proof: Under the assumptions of the claim, p + 1 is divisible by 4, so (p + 1)∕4 is an integer. Then

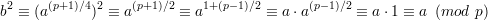
by the Euler Criterion (Claim 3). __

66 Shank’s Algorithm for Finding Square Roots Modulo Odd Primes

Let p be an odd prime. Let s and t be unique integers such that p - 1 = 2^st and t is odd. (Note that s is simply the number of trailing 0’s in the binary expansion of p - 1, and t is what remains when p - 1 is shifted right by s places.) Because p is odd, p - 1 is even, so s ≥ 1.

In the special case when s = 1, p- 1 = 2t, so p = 2t + 1. Writing the odd number t as 2ℓ + 1 for some integer ℓ, we have p = 2(2ℓ + 1) + 1 = 4ℓ + 3, so p ≡ 3 (mod 4). But this is exactly the special that we considered in Section 65.

We now present an algorithm that works to find square roots of quadratic residues modulo any odd prime p. Algorithm 66.1, due to D. Shanks² , bears a strong resemblance to Algorithm 56.1 for factoring the RSA modulus given both the encryption and decryption exponents.

Let p,s,t be as above. Assume a QR_p is a quadratic residue and u QNR_p is a quadratic non-residue. (We can easily find u by choosing random elements of Z*_p and applying the Euler Criterion.) The goal is to find x such that x² ≡ a (mod p).

Shank’s Algorithm Input: Odd prime p, quadratic residue a QRp. Output: A square root of a (mod p). 1. Let s, t satisfy p = 2st and t odd. 2. Let u QNRp. 3. k = s 4. z = ut mod p 5. x = a(t+1)∕2 mod p 6. b = at mod p 7. while (b ⁄≡ 1 (mod p)) { 8. let m be the least integer with b2m ≡ 1 (mod p) 9. t = z2k-m-1 mod p 10. z = t2 mod p 11. b = bz mod p 12. x = xt mod p 13. k = m 14. } 15. return x Figure 66.1: Shank’s algorithm for finding a square root of a (mod n).

The congruence x² ≡ ab (mod p) is easily shown to be a loop invariant. It’s clearly true initially since x² ≡ a^t+1 and b ≡ a^t (mod p). Each time through the loop, a is unchanged, b gets multiplied by t² (lines 10 and 11), and x gets multiplied by t (line 12); hence the invariant remains true regardless of the value of t. If the program terminates, we have b ≡ 1 (mod p), so x² ≡ a, and x is a square root of a (mod p).

To see why it terminates after at most s iterations of the loop, we look at the orders³ of b and z (mod p) at the start of each loop iteration (before line 8) and show that ord(b) < ord(z) = 2^k.

On the first iteration, k = s, and z ≡ u^t (mod p). We argue that ord(z) = 2^s. Clearly

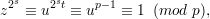
so ord(z)∣2^s. By the Euler Criterion, since u is a non-residue, we have

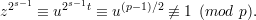
Hence, ord(z) = 2^s. Using similar reasoning, since a is a quadratic residue, b^2s-1 ≡ 1 (mod p), so ord(b)∣2^s-1. It follows that ord(b) < ord(z) = 2^s = 2^k.

Now, on each iteration, line 8 sets m = ord(b) and line 9 sets t = z^2k-m-1 mod p, so

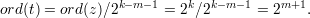
Line 10 sets z = t², so ord(z) = ord(t)∕2 = 2^m. After line 11, ord(b) < 2^m. This because the old value of b and the new value of z both have order 2^m. Hence, both of those numbers raised to the power 2^m-1 are -1 (mod p), so their product (the new value of b) raised to that same power is (-1)² ≡ 1. Line 13 sets k = m in preparation for the next iteration, and the loop invariant ord(b) < ord(z) = 2^k is maintained. Moreover, ord(b) is reduced at each iteration, so the loop must terminate after at most s iterations.

67 QR Probabilistic Cryptosystem

Let n = pq, p, q distinct odd primes. We can divide the numbers in Z*_n into four classes depending on their membership in QR_p and QR_q.⁴ Let Q_n¹¹ be those numbers that are quadratic residues mod both p and q; let Q_n¹⁰ be those numbers that are quadratic residues mod p but not mod q; let Q_n⁰¹ be those numbers that are quadratic residues mod q but not mod p; and let Q_n⁰⁰ be those numbers that are neither quadratic residues mod p nor mod q. Under these definitions, Q_n¹¹ = QR_n and Q_n⁰⁰ ∪ Q_n⁰¹ ∪ Q_n¹⁰ = QNR_n. Fact Given a Q_n⁰⁰ ∪Q_n¹¹, there is no known feasible algorithm for determining whether or not a QR_n that gives the correct answer significantly more than 1/2 the time.

The Goldwasser-Micali cryptosystem is based on this fact. The public key consist of a pair e = (n,y), where n = pq for distinct odd primes p, q, and y Q_n⁰⁰. The private key consists of p. The message space is 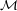= {0,1}.

To encrypt m 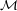, Alice chooses a random a QR_n. She does this by choosing a random member of Z*_n and squaring it. If m = 0, then c = a mod n. If m = 1, then c = ay mod n. The ciphertext is c.

It is easily shown that if m = 0, then c Q_n¹¹, and if m = 1, then c Q_n⁰⁰. One can also show that every element of Q_n¹¹ is equally likely to be chosen as the ciphertext c in case m = 0, and every element of Q_n⁰⁰ is equally likely to be chosen as the ciphertext c in case m = 1. Eve’s problem of determining whether c encrypts 0 or 1 is the same as the problem of distinguishing between membership in Q_n⁰⁰ and Q_n¹¹, which by the above fact is believed to be hard. Anyone knowing the private key p, however, can use the Euler Criterion to quickly determine whether or not c is a quadratic residue mod p and hence whether c Q_n¹¹ or c Q_n⁰⁰, thereby determining m.