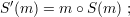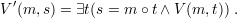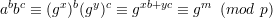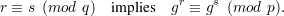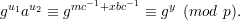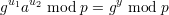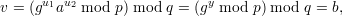YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 467a: Cryptography and Computer Security | Notes 18 (rev. 1) |
| Professor M. J. Fischer | | November 10, 2008 |
|
|
|
| |
79 Brief Review of Squares and Square Roots
We have discussed several results about quadratic residues and square roots modulo odd primes and
modulo composite numbers, particularly for the special case of the product of two distinct odd primes. I
want to summarize these results to help you keep them straight and to give a greater perspective on how
they relate to each other.
79.1 Testing versus computing
Testing for the existence of an element with specific properties is never harder than finding it, and it can be
much easier. For example, finding a proper prime divisor of a number n is equivalent to the factoring
problem, a problem believed to be intractable. On the other hand, testing for the existence of a proper prime
divisor of n is equivalent to testing if n is prime, a problem for which we have shown feasible probabilistic
solutions.
Similarly, testing if a number a is a quadratic residue modulo n is the same thing as testing if it has a
square root modulo n. This problem is never harder than the problem of finding a square root since, given
the ability to find square roots, one can test if a has a square root by trying to find it! If one succeeds, then a
is definitely a quadratic residue. If one fails, then either it’s because a doesn’t have a square root or because
the algorithm doesn’t always work and therefore isn’t really a solution to the problem. Of course, an
algorithm can fail by running a long time without halting, so in order to infer that a is not a quadratic
residue, we must be able to detect that our square root algorithm has failed, either because it has explicitly
halted with a failure indication, it has produced an incorrect answer that we can verify is wrong,
or it has already run longer on the given input than it runs on any quadratic residue of that
length.
79.2 Prime versus composite modulus
When the modulus is an odd prime p, testing for existence of and finding square roots are both easy. Testing
is simply done using the Euler Criterion (section 64, lecture notes 15). Square roots can be found using
Shank’s algorithm (section 66, lecture notes 15).
When the modulus n = pq is the product of two distinct odd primes p and q and both are known, the
proof of Claim 2 (section 63, lecture notes 15) establishes that a is a quadratic residue modulo n if and
only if it is a quadratic residue modulo both p and q. It also indicates how to use the Chinese Remainder
theorem to find a square root of a modulo n given square roots bp and bq of a modulo p and q,
respectively.
On the other hand, when n = pq but p and q are not known, no feasible algorithm is known for testing
if an arbitrary number is a quadratic residue modulo n. Here the situation is a bit more complicated, for it is
easy for 1/2 of the numbers in Z*
n to determine that they are not quadratic residues modulo n. Namely, the
numbers with Jacobi symbol  = -1 are exactly the numbers a
= -1 are exactly the numbers a  Qn01 ∪ Qn10 which are quadratic
residues modulo one of p or q but not both. (See section 67, lecture notes 15.) The Jacobi symbol
is easily computed by the method of section 70, lecture notes 16. However, the numbers in
a
Qn01 ∪ Qn10 which are quadratic
residues modulo one of p or q but not both. (See section 67, lecture notes 15.) The Jacobi symbol
is easily computed by the method of section 70, lecture notes 16. However, the numbers in
a  Qn00 ∪ Qn11 all have Jacobi symbol 1, but half of them are quadratic residues modulo n
wherease the other half are not, and there is no known feasible algorithm for distinguishing the
quadratic residues from the non-residues. This is the basis for the Goldwasser-Micali cryptosystem
presented in section 67, lecture notes 15. It follows from the remarks in section 79.1 above that
also no feasible algorithm is known for computing square roots of quadratic residues modulo
n.
Qn00 ∪ Qn11 all have Jacobi symbol 1, but half of them are quadratic residues modulo n
wherease the other half are not, and there is no known feasible algorithm for distinguishing the
quadratic residues from the non-residues. This is the basis for the Goldwasser-Micali cryptosystem
presented in section 67, lecture notes 15. It follows from the remarks in section 79.1 above that
also no feasible algorithm is known for computing square roots of quadratic residues modulo
n.
80 Combining Signatures with Encryption
One often wants to encrypt messages for privacy and sign them for integrity and authenticity. Suppose
Alice has a cryptosystem (E,D) and a signature system (S,V ). Three possibilities come to mind for
encrypting and signing a message m:
- Alice signs the encrypted message, that is, she sends (E(m),S(E(m))).
- Alice encrypts the signed message, that is, she sends E(m ∘ S(m)). Here we assume a
standard way of representing the ordered pair (m,S(m)) as a string, which we denote by
m ∘ S(m).
- Alice encrypts only the first component of the signed message, that is, she sends the pair
(E(m),S(m)).
Note that method 3 is quite problematic since signature functions make no guarantee of privacy. In
particular, if (S,V ) is, say, an RSA signature scheme, we can define a new signature scheme
(S′,V ′):
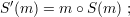
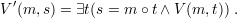
Clearly, the ability to forge signatures in (S′,V ′) implies the ability to forge signatures in
(S,V ), for if (m,s) is a valid signed message in (S′,V ′), then (m,t) is a valid signed message
in (S,V ), where t is the second component of the ordered pair encoded by s. Thus, the new
scheme is at least as secure as the original. But with (S′,V ′), the plaintext message is part of the
signature itself, so if (S′,V ′) is used as the signature scheme in method 3 above, there is no
privacy.
Think about the pros and cons of the other two possibilities. For example, method 1 allows a third
party to verify that the encrypted message was signed by Alice even without being able to decrypt it.
Whether or not this is desirable is application-dependent. The point is, subtlties emerge when cryptographic
protocols are combined, even in a simple case like this where it is only desired to combine privacy with
authentication.
81 ElGamal Signatures
The ElGamal signature scheme uses ideas similar to those of his encryption system, which we have already
seen. The private signing key consists of a primitive root g of a prime p and an exponent x. The public
verification key consists of g, p, and the number a = gx mod p. The signing and verification algorithms are
given below:
| To sign m:
|
| 1. | Choose random y  Z*ϕ(p). Z*ϕ(p). |
| 2. | Compute b = gy mod p. |
| 3. | Compute c = (m - xb)y-1 mod ϕ(p). |
| 4. | Output signature s = (b,c). |
| To verify (m,s), where s = (b,c):
|
| 1. | Check that abbc ≡ gm (mod p). |
Why does
this work? Plugging in for a and b, we see that
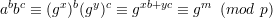
since xb + yc ≡ m (mod ϕ(p)).
82 Digital Signature Algorithm (DSA)
The commonly-used Digital Signature Algorithm (DSA) is a variant of ElGamal signatures. Also called the
Digital Signature Standard (DSS), it is described in U.S. Federal Information Processing Standard FIPS
186–2. It uses two primes:
p, which is 1024 bits long,
and q, which is 160 bits long and satisfies q∣(p - 1). Here’s how to find them: Choose q first, then
search for z such that zq + 1 is prime and of the right length. Choose p = zq + 1 for such a
z.
Now let g = h(p-1)∕q mod p for any h  Z*p for which g > 1. This ensures that g
Z*p for which g > 1. This ensures that g  Z*p is a
non-trivial qth root of unity modulo p. Let x
Z*p is a
non-trivial qth root of unity modulo p. Let x  Z*q and compute a = gx mod p. The parameters p, q, and g
are common to the public and private keys. In addition, the private signing key contains x and the public
verification key contains a.
Z*q and compute a = gx mod p. The parameters p, q, and g
are common to the public and private keys. In addition, the private signing key contains x and the public
verification key contains a.
Here’s how signing and verification work:
| To sign m:
|
| 1. | Choose random y  Z*q. Z*q. |
| 2. | Compute b = (gy mod p) mod q. |
| 3. | Compute c = (m + xb)y-1 mod q. |
| 4. | Output signature s = (b,c). |
| To verify (m,s), where s = (b,c):
|
| 1. | Verify that b,c  Z*q; reject if not. Z*q; reject if not. |
| 2. | Compute u1 = mc-1 mod q. |
| 3. | Compute u2 = bc-1 mod q. |
| 4. | Compute v = (gu1au2 mod p) mod q. |
| 5. | Check v = b. |
To see why this works, note that since gq ≡ 1 (mod p), then
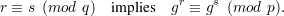
This follows from the fact that g is a qth root of unity modulo p, so gr+uq ≡ gr(gq)u ≡ gr (mod p) for
any u. Hence,
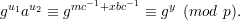
It follows that
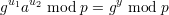
and hence
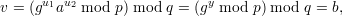
as desired. (Notice the shift between equivalence modulo p and equality of remainders modulo
p.)
Remarks
DSA introduces this new element of computing a number modulo p and then modulo q. Call this function
fp,q(n) = (n mod p) mod q. This is not the same as n mod r for any number r, nor is it the same as
(n mod q) mod p.
To understand better what’s going on, let’s look at an example. Take p = 29 and q = 7.
Then 7|(29 - 1), so this is a valid DSA prime pair. The table below lists the first 29 values of
y = f29,7(n):
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| y | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
The sequence of function values repeats after this point with a period of length 29. Note that it both begins and
ends with 0, so there is a double 0 every 29 values. That behavior cannot occur modulo any number r.
That behavior is also different from f7,29(n), which is equal to n mod 7 and has period 7.
(Why?)
 = -1 are exactly the numbers a
= -1 are exactly the numbers a  Qn01 ∪ Qn10 which are quadratic
residues modulo one of p or q but not both. (See section 67, lecture notes 15.) The Jacobi symbol
is easily computed by the method of section 70, lecture notes 16. However, the numbers in
a
Qn01 ∪ Qn10 which are quadratic
residues modulo one of p or q but not both. (See section 67, lecture notes 15.) The Jacobi symbol
is easily computed by the method of section 70, lecture notes 16. However, the numbers in
a  Qn00 ∪ Qn11 all have Jacobi symbol 1, but half of them are quadratic residues modulo n
wherease the other half are not, and there is no known feasible algorithm for distinguishing the
quadratic residues from the non-residues. This is the basis for the Goldwasser-Micali cryptosystem
presented in section 67, lecture notes 15. It follows from the remarks in section 79.1 above that
also no feasible algorithm is known for computing square roots of quadratic residues modulo
n.
Qn00 ∪ Qn11 all have Jacobi symbol 1, but half of them are quadratic residues modulo n
wherease the other half are not, and there is no known feasible algorithm for distinguishing the
quadratic residues from the non-residues. This is the basis for the Goldwasser-Micali cryptosystem
presented in section 67, lecture notes 15. It follows from the remarks in section 79.1 above that
also no feasible algorithm is known for computing square roots of quadratic residues modulo
n.