83 Common Hash Functions

Many cryptographic hash functions are currently in use. For example, the openssl library includes implementations of MD2, MD4, MD5, MDC2, RIPEMD, SHA, SHA–1, SHA–256, SHA–384, and SHA–512. The SHA–xxx methods are recommended for new applications, but these other functions are also in widespread use.

83.1 SHA–1

The revised Secure Hash Algorithm (SHA–1) is one of four algorithms described in U. S. Federal Information Processing Standard FIPS PUB 180–2 (Secure Hash Standard).¹ It states,

SHA–1 produces a 160-bit message digest. The other algorithms in the SHA–xxx family produce longer message digests.

83.2 MD5

MD5 is an older algorithm (1992) devised by Rivest. We present an overview of it here. It generates a 128-bit message digest from an input message of any length. It is built from a basic block function g : 128-bit × 512-bit → 128-bit.

The MD5 hash function h is obtained as follows: First the original message is padded to length a multiple of 512. The result m is split into a sequence of 512-bit blocks m₁,m₂,…,m_k. Finally, h is computed by chaining g on the first argument.

We look at these steps in greater detail. As with block encryption, it is important that the padding function be one-to-one, but for a different reason. For encryption, the one-to-one property is what allows unique decryption. For a hash function, it prevents there from being trivial colliding pairs. For example, if the last partial block is simply padded with 0’s, then all prefixes of the last message block will become the same after padding and will therefore collide with each other.

The function h can be regarded as a state machine, where the states are 128-bit strings and the inputs to the machine are 512-bit blocks. The machine starts in state s₀, specified by an initialization vector IV. Each input block m_i takes the machine from state s_i-1 to new state s_i = g(s_i-1,m_i). The last state s_k is the output of h, that is,

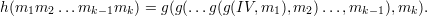
The block function g(s,b) is built from a scrambling function g′(s,b) that regards s and b as sequences of 32-bit words and returns four 32-bit words as its result. Suppose s = s₁s₂s₃s₄ and g′(s,b) = s′₁s′₂s′₃s′₄. Then we define

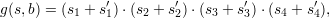
where “+” means addition modulo 2³² and “⋅” is concatenation of the representations of integers as 32-bit binary strings.

The computation of the scrambling function g′(s,b) consists of 4 stages, each consisting of 16 substages. We divide the 512-bit block b into 32-bit words b₁b₂…b₁₆. Each of the 16 substages of stage i uses one of the 32-bit words of b, but the order they are used is defined by a permutation π_i that depends on i. In particular, substage j of stage i uses word b_ℓ, where ℓ = π_i(j) to update the state vector s. The new state is f_i,j(s,b_ℓ), where f_i,j is a bit-scrambling function that depends on i and j.

Without going into further details of the functions f_i,j, we note that the state s can be represented by four 32-bit words, so the arguments to f_i,j occupy only 5 machine words. These easily fit into the high-speed registers of modern processors.

The definitive specification for MD5 is RFC1321 and errata. A general discussion of MD5 along with links to recent work and security issues can be found on Wikipedia.

84 Doubling Reduction Amount of Hash Functions

Suppose we are given a particular fixed-length hash function h : 256-bits → 128-bits. How can we use h to compute a 128-bit strong collision-free hash of a 512-bit input block? We consider several possible ways to extend h to a hash function H : 512-bits → 128-bits. In the following, we suppose that m is 512-bits long, and we write M = m₁m₂, where m₁ and m₂ are 256 bits each.

Method 1

Define H(M) = H(m₁m₂) = h(m₁) ⊕ h(m₂). Unfortunately, this fails to be either strong or weak collision-free since M′ = m₂m₁ always collides with M under H except in the special case that m₁ = m₂.

Method 2

Define H(M) = H(m₁m₂) = h(h(m₁)h(m₂)).

Theorem 1 The H of method 2 is strong collision-free assuming that the h from which it is derived is strong collision-free.

Proof: Assume the contrary, that one can find a colliding pair (M,M′) for H. We show that one can then find a colliding pair for h, contradicting the assumption that h is strong collision-free.

Write M = m₁m₂ and M′ = m′₁m′₂ for 256-bit blocks m₁,m₂,m′₁,m′₂. Since M collides with M′, we have that M≠M′ but H(M) = H(M′). We consider two cases.

Case 1: h(m₁)≠h(m′₁) or h(m₂)≠h(m′₂). Let u = h(m₁)h(m₂) and u′ = h(m′₁)h(m′₂). Then u≠u′, but h(u) = H(M) = H(M′) = h(u′), so (u,u′) is a colliding pair for h.

Case 2: h(m₁) = h(m′₁) and h(m₂) = h(m′₂). Since m≠m′, then either m₁≠m′₁ or m₂≠m′₂ (or both). But then whichever pair is unequal is a colliding pair for h.

In either case, we have found a colliding pair for h, contradicting the assumption that h was strong collision-free. __

85 A General Chaining Method for Constructing Hash Functions

Assume now that we have a hash function h : r-bits → t-bits, where r ≥ t + 2. In the above example, r = 256 and t = 128. Divide the message m after appropriate padding into blocks m₁m₂…m_k, each of length r - t - 1. Compute a sequence of t-bit states as follows:

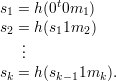
Then H(m) = s_k.

Proof: Assume to the contrary that H is not strong collision-free, so we are able to find a colliding pair (m,m′) for H. We show how to find a colliding pair for h, contradicting the assumed collision-freedom of h.

Let m = m₁m₂…m_k, let m′ = m′₁m′₂…m′_k′, and let s₁,…,s_k and s′₁,…,s′_k′ be the corresponding state sequences. We may assume without loss of generality that k ≤ k′. Because m and m′ collide under H, we have s_k = s′_k′. Let i be the least integer in {1,…,k} such that, for all j {i,…,k}, we have s_j = s′_k′-k+j. Such an i exists since i = k is one value that works. We proceed by cases:

Case 1:  i = 1 and k = k′. Then s_j = s′_j for all j = 1,…,k. Because m≠m′, there must be some ℓ such that m_ℓ≠m′_ℓ. If ℓ = 1, then (0^t0m₁,0^t0m′₁) is a colliding pair for h. If ℓ > 1, then (s_ℓ-11m_ℓ, s′_ℓ-11m′_ℓ) is a colliding pair for h.

Case 2:  i = 1 and k < k′. Let u = k′- k + 1. Then s₁ = s′_u. Since u > 1 we have that

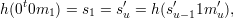
so (0^t0m₁, s′_u-11m′_u) is a colliding pair for h. Note that this is true even if 0^t = s′_u-1 and m₁ = m′_u, a possibility that we have not ruled out.

Case 3:  i > 1. Then u = k′- k + i > 1. By the definition of i, we have s_i = s′_u, but s_i-1≠s′_u-1 since i was chosen to be as small as possible. Hence,

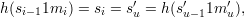
so (s_i-11m_i, s′_u-11m′_u) is a colliding pair for h.

In each case, we have found a colliding pair for h. The contradicts the assumption that h is strong collision-free. Hence, H is also strong collision-free. __

86 Hash Functions Do Not Always Look Random

Intuitively, we like to think of h(y) as being “random-looking”, with no obvious pattern. Indeed, it would seem that obvious patterns and structure in h would provide a means of finding collisions, violating the property of being strong-collision free. But this intuition is faulty, as I now show.

Suppose h is a strong collision-free hash function. Define H(x) = 0 ⋅ h(x). Clearly, H also enjoys these same properties. If (x₁,x₂) is a colliding pair for H, then it is also a colliding pair for h. Thus, H is strong collision-free, despite the fact that the string H(x) always begins with 0. Later on, we will talk about how to make functions that truly do appear to be random (even though they are not).

87 Birthday Attack on Hash Functions

Recall that the MD5 hash function produces 128-bit values, whereas SDA–1 produces 160-bit values. How many bits do we need for security? Both 2¹²⁸ and 2¹⁶⁰ are more than large enough to thwart a brute force attack that simply searches randomly for colliding pairs (m,m′). However, the so-called Birthday Attack reduces the size of the search space to roughly the square root of the original size. Thus, MD5 has roughly the same resistance to the birthday attack as a cryptosystem with 64-bit keys would have to a brute force attack. Similarly, SHA–1’s effective size in terms of birthday attack resistance is only 80-bits.²

We saw an example of a birthday attack in section 26 of lecture notes 5. The birthday attack is named for the birthday paradox. This is the fact that there is approximately a 50–50 chance that two people in a room of 23 strangers have the same birthday. There is a nice description of the birthday paradox on the web at http://en.wikipedia.org/wiki/Birthday_paradox. The probability of not having two people with the same birthday is is

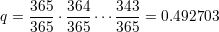
Hence, the probability that (at least) two people have the same birthday is 1 - q = 0.507297. This probability grows quite rapidly with the number of people in the room. For example, with 46 people, the probability that two share a birthday is 0.948253.

The birthday paradox can be applied to hash functions to yield a much faster way to find colliding pairs than choosing pairs at random. The idea is to choose a random set of k messages and then see if any two messages in the set collide. There are (k 2) = k(k - 1)∕2 different pairs of messages in a set of size k, so on can test this many pairs at a cost of only k evaluations of the hash function. Of course, these (k 2) pairs are not uniformly distributed, so one needs a birthday-paradox style analysis of the probability that a colliding pair will be found. The general result is that the probability of success is at least one half for k roughly the size of 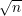, where n is the size of the message space.

Two problems remain that make this attack difficult to use in practice. First, there is the problem of finding duplicates in the list of hash values. That can be done in time O(k log k) by sorting the list and then looking for adjacent equal elements. The more serious problem with this approach, and with the birthday attack in general, is the amount of storage required. While carrying out 2⁶⁴ computational steps is almost on the verge of feasibility, finding that much storage is still way out of the question, so MD5 and other 128-bit hash functions are still safe from this attack. Nevertheless, the birthday attack is one of the more subtle ways that cryptographic primitives can be compromised.

88 Hash from Cryptosystem

We’ve already seen several cryptographic hash functions as well as methods for making new hash functions from old. Here’s a way to make a hash function from a symmetric cryptosystem with encryption function E_k(b). Assume that the key length and block length are the same. Let m be an arbitrary length message. Pad it appropriately and divide it into block lengths appropriate for the cryptosystem. Compute the following state sequence:

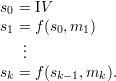
The output H(m) of the new hash function is s_k. IV is an initial vector and f is a function built from E. Some possibilities for f are

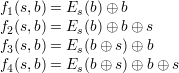
You should think about why these particular functions do or do not lead to a strong collision-free hash function. For example, if k = 1 and f = f₁, then H₁(b) = E_IV (b) ⊕b. E_IV itself is one-to-one (since it’s an encryption function), but what can we say about H₁(b)? Indeed, if bad luck would have it that E_IV is the identity function, then H₁(b) = 0 for all b, and all pairs of message blocks collide!