89 Authentication Problem

The authentication problem is to identify who one is communicating with. For example, if Alice and Bob are communicating over a network, then Bob would like to know that he is talking to Alice and not to someone else on the network. Knowing the IP address or URL is not adequate since Mallory might be in control of intermediate routers and name servers.

As with signature schemes, we need some way to differentiate the real Alice from other users of the network. We generally do this by assuming that Alice possess some secret or password that is not known to anyone else. Then Alice authenticates herself by proving that she knows the secret password.

90 Passwords

Password mechanisms are widely used for authentication. In the usual form, Alice authenticates herself by sending her password to Bob. Bob checks that it matches Alice’s password and grants access. This is the scheme that is used for local logins to a computer and is also used for remote authenticated telnet, ftp, rsh, and rlogin sessions. Such schemes have two major security weaknesses:

1. Except for local logins, the password is sent over the network in the clear. This exposes it to various kinds of eavesdropping, ranging from ethernet packet sniffers on the LAN to corrupt ISP’s and routers along the way. The real threat of password capture in this way is so great that it is highly recommended that one never send a password over the internet in the clear. Users of the old insecure Unix tools should switch to secure replacements such as ssh, slogin, and scp, or kerberized versions of telnet and ftp.

   Logins into web sites often use the SSL (Secure Socket Layer) protocol to encrypt the connection, making it safe to transmit passwords to the site, but some do not. Depending on how you have it configured, your browser will warn you whenever you attempt to send unencrypted data back to the server.

2. Even if the password reaches the server safely, it is no longer the case that Alice is the only one who knows her password. Now the server also knows. This is no problem if the only use of the password is to authenticate Alice to that particular server, but what it means is that from then on, the server can impersonate Alice to any other service that uses the same password.

   Users these days may have accounts with dozens of different web sites. In order make the task of remembering the user names and passwords on all those sites, one is tempted to use the same user name-password pairs on all of them. But that means that anyone with access to the password database on one site could log into Alice’s account on any of the other sites. Typically the different sites have very differing sensitivity of the data they protect. An on-line shopping site may only be protecting a customer’s shopping cart, whereas a banking site allows access to a customer’s bank account.

   My advice is to use a different password for each account. Of course, nobody can keep dozens of different passwords straight, so the downside of my suggestion is that the passwords must be written down and kept safe. If the primary paper on which they are written gets lost, then one should have a backup copy so that one can go to all of the sites ASAP and change the passwords (and learn if the site has been compromised).

The real problem with simple password schemes is that Alice is required to send her secrets to other parties in order to use them. We will see in the next lecture authentication schemes that do not require this.

91 Secure Password Storage

Another issue with traditional password authentication schemes is the necessity of storing the passwords on the server for later verification. The file in which the passwords are stored is obviously highly sensitive. While operating system protections can (and should) be used to protect it, they are not really sufficient. For one thing, legitimate sysadmins can access it and might conceivably use the passwords found there to log into users’ accounts at other sites. Hackers who manage to break into the computer and obtain root privileges could also do the same thing. Finally, files get copied onto backup tapes that are not subject to the same system protections, so someone with access to a backup tape could read everybody’s password from it.

Rather than store passwords in the clear, it is usual to store “encrypted” passwords, which really means the hash value of the password under some cryptographic hash function. The authentication function takes the cleartext password from the user, computes its hash value, and sees if that matches the hashed value in the password file. Since the password does not contain the actual password, and it is computationally difficult to invert a cryptographic hash function, knowledge of the hash value does not allow an attacker to easily find the password.

92 Dictionary Attacks

Nevertheless, access to the password file, even if only hashed passwords are stored, opens up the possibility of a dictionary attack. The idea here is that many users choose weak passwords—words that appear in an English dictionary or in other available sources of text. If one has access to the password hashes of legitimate users on the computer (such as is contained in /etc/passwd on Unix), an attacker can hash every word in the dictionary and then look for matches with the password file entries. This attack is quite likely to succeed in compromising at least a few accounts on a typical system. Even one compromised account is enough to allow the hacker to log into the system as a legitimate user, from which other kinds of attacks are possible that cannot be carried out from the outside.

A way to make dictionary attacks more expensive is to add salt to each password. Salt is a random number that is attached to a user’s account and stored along with the user name and hashed password in the password file. The hash function takes two arguments, the password and salt, and produces a hash value. Because the salt is stored (in the clear) in the password file, the user’s password can be easily verified. However, a particular password hashes in different ways depending on the salt value. This means that a successful dictionary attack would have to encrypt the entire dictionary with every possible salt value (or at least with every salt value that appeared in the password file being attacked). This increases the cost of the attack by orders of magnitude.

93 Authentication While Preventing Impersonation

A fundamental problem with all of the password authentication schemes discussed so far is that Alice reveals her secret to Bob every time she authenticates herself. This is fine in an environment where she trusts Bob but not otherwise, for after authenticating herself once to Bob, then Bob can in turn masquerade as Alice to others.

When neither Alice nor Bob trust each other, there are two requirements that must be met:

1. Bob wants to make sure that an impostor cannot successfully masquerade as Alice.
2. Alice wants to make sure that her secret remains secure.

At first sight these seem contradictory, but there actually are ways for Alice to prove her identity to Bob without compromising her secret.

94 Challenge-response authentication protocols

In a challenge-response protocol, Bob presents Alice with a challenge that only the true Alice (someone knowing Alice’s secret) can answer. Alice answers the challenge and sends her answer to Bob, who verifies that it is correct.

A challenge-response protocol can be built from a digital signature scheme (S_A,V _A) as shown in Figure 94.1. (The same protocol can also be implemented using a symmetric cryptosystem with shared key k.)

Alice Bob 1. Choose random string r. 2. Compute s = SA(r) Check V A(r,s). Figure 94.1: Simple challenge-response protocol.

The problem with this protocol is that it exposes Alice’s signature system to a chosen plaintext attack. With this protocol, a malicious Bob can get Alice to sign any message of his choosing. Among other things, this means that Alice had better have a different signing key for use with this protocol than she uses to sign contracts.

While we hope our cryptosystems are resistant to chosen plaintext attacks, such attacks are very powerful and are not easy to defend against. Anything we can do to limit exposure to such attacks can only improve the security of the system.

We now look at some ways that Alice might limit Bob’s ability to carry out a chosen plaintext attack. In the protocol of Figure 94.2, instead of signing a string r of Bob’s choice, Alice signs a string r that is constructed from a part r₁ chosen by Alice and a part r₂ chosen by Bob.

Alice Bob 1. Choose random string r1 2. Choose random string r2. 3. Compute r = r1 ⊕ r2 Compute r = r1 ⊕ r2 4. Compute s = SA(r) Check V A(r,s). Figure 94.2: Attempt to resist chosen plaintext attack: Alice goes first.

The idea is that neither party be able to control r. Unfortunately, that idea does not work here because Bob gets r₁ before choosing r₂. Instead of choosing r₂ randomly, a cheating Bob can choose r₂ = r ⊕r₁, where r is the string that he wants Alice to sign as part of his chosen plaintext attack on her cryptosystem. Thus, the protocol of Figure 94.2 is no more secure against chosen plaintext attack than the simpler protocol of Figure 94.1.

Another possibility is to choose the random strings in the other order—Bob chooses first and then Alice—giving the protocol of Figure 94.3.

Alice Bob 1. Choose random string r2. 2. Choose random string r1 3. Compute r = r1 ⊕ r2 Compute r = r1 ⊕ r2 4. Compute s = SA(r) Check V A(r,s). Figure 94.3: Attempt to resist chosen plaintext attack: Bob goes first.

Now Alice is the one who has complete control over r. This indeed thwarts Bob’s chosen plaintext attack since r is completely random (i.e., all strings r are equally likely). No matter how Bob chooses r₂, Alice choice of a random string r₁ ensures that r is also random. Thus, Alice only signs random messages.

Unfortunately, the protocol of Figure 94.3 is totally insecure against active eavesdroppers. Suppose Mallory listens to a legitimate execution of the protocol between Alice and Bob. From this, he easily acquires a valid signed message (r₀,s₀). Now Mallory can impersonate Alice by choosing r₁ = r₀ ⊕r₂ in step 2 and s = s₀ in step 4. Bob computes r = r₁ ⊕ r₂ = r₀ in step 3, so his verification in step 4 succeeds.

Both of these protocols can be improved by letting r be r₁ ⋅r₂ (concatenation) instead of r₁ ⊕r₂. That way, neither party has full control over r. This weakens Bob’s ability to launch a chosen plaintext attack in the protocol of Figure 94.2, and it weakens Mallory’s ability to impersonate Alice in the protocol of Figure 94.3. A still better idea might be to let r = h(r₁ ⋅ r₂), where h is a cryptographic hash function, since this further weakens the control that either party has on the choice of r.

95 Feige-Fiat-Shamir Authentication Protocol

In all of the challenge-response protocols above, Alice releases some partial information about her secret by producing signatures that Bob could not compute by himself. As we will see, the Feige-Fiat-Shamir protocol allows Alice to prove knowledge of her secret without revealing any information about the secret itself. Such protocols are called zero knowledge, which we will discuss in subsequent lectures.

The Feige-Fiat-Shamir protocol is based on the difficulty of computing square roots modulo composite numbers. Alice chooses n = pq, where p and q are distinct large primes. Next she picks a quadratic residue v QR_n (which she can easily do by choosing a random element u and letting v = u² mod n). Finally, she chooses s to be the smallest square root of v^-1 (mod n).¹ She can do this since she knows the factorization of n. She makes n and v public and keeps s private.

Alice authenticates herself by successfully completing a protocol that requires knowledge of s. We present a simplified version of the protocol in Figure 95.1. In a single round of the protocol, Bob has at least a 50% chance of catching an impostor Mallory. By repeating the protocol t times, the error probability (that is, the probability that Bob fails to catch Mallory) drops to 1∕2^t. This can be made acceptably low by choosing t to be large enough. For example, if t = 20, then Mallory has only one chance in a million of successfully impersonating Alice.

Alice Bob 1. Choose random r Zn. Compute x = r2 mod n. 2. Choose random b {0,1}. 3. Compute y = rsb mod n. Check x = y2vb mod n. Figure 95.1: One round of the simplified Feige-Fiat-Shamir authentication protocol.

To see that this works when both parties are honest, we just have to verify that

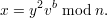(1)

But this follows since

95.1 Cheating Alice

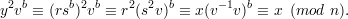
We now turn to the security properties of the protocol when Alice is dishonest, that is, when a party Mallory is attempting to impersonate Alice.

Proof: In order for Mallory to successfully fool Bob, he must come up with x in step 1 and y in step 3 satisfying (1). He does not know which value b Bob will choose when he is sends x in step 1. Let y_b be the string that Mallory sends to Bob in response to query b. We consider two cases.

Case 1: There is at least one b {0,1} for which y_b fails to satisfy (1). Since b = 0 and b = 1 each occur with probability 1/2, this means that Bob’s verification will fail with probability at least 1/2, as desired.

Case 2: y₀ and y₁ both satisfy (1) (for their respective values of b), so we have

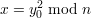
and

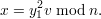
We can solve these equations for v^-1 to get

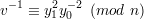
But then y₁y₀^-1 mod n is a square root of v^-1. Since Mallory was able to compute both y₁ and y₀, then he was also able to compute a square root of v^-1, contradicting the assumption that he doesn’t “know” a square root of v^-1. __

We remark that it is possible for Mallory to cheat with success probability 1/2. Here’s what he does. He guesses the bit b that Bob will send him in step 2. He then generates a pair (x,y). If he guesses b = 0, then he chooses x = r² mod n and y = r mod n, just as Alice would have. If he guesses b = 1, then he chooses y arbitrarily and x = y²v mod n. He then sends x in step 1 and y in step 3. The pair (x,y) passes Bob’s check if Mallory’s guess of b turns out to be correct, which will happen probability 1/2.

95.2 Cheating Bob

We now consider the case of a dishonest Mallory impersonating Bob. Alice would like assurance that if she follows the protocol, her secret is protected, regardless of what Bob does.

Consider what Mallory knows at the end of the protocol. If he sent b = 0 in step 2, then he ends up with a pair (x,y), where x is a random number and y is its square modulo n. Neither of these numbers depend in any way on Alice secret s, so it’s intuitively obvious that this gives Mallory no direct information about s. It’s also of no conceivable use to Mallory in trying to find s by other means, for he can compute such pairs by himself without involving Alice. If having such pairs allows him find a square root of v^-1, then he was already able to compute square roots, contrary to the assumption that finding square roots modulo n is difficult.

Instead, suppose Mallory sent b = 1 in step 2. Now he ends up with the pair (x,y), where x = r² mod n and y = rs mod n. While y might seem to give information about s, observe that y itself is just a random element of Z_n. This is because r is random, and the mapping r → rs mod n is one-to-one for all s Z*_n. Hence, as r ranges through all possible values, so does rs mod n. What does Mallory learn from x? Nothing that he could not have computed himself knowing y, for x = y²v mod n. So again, all he ends up with is a random number (y in this case) and a quadratic residue that he can compute knowing y.

In both cases, Mallory ends up with information that he could have computed without interacting with Alice. Hence, if he could have discovered Alice’s secret by talking to Alice, then he could have also done so on his own, contradicting the hardness assumption for computing square roots. This is the sense in which Alice’s protocol releases zero knowledge about her secret.