|
|
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 21 (rev. 1) | |
| Professor M. J. Fischer | November 19, 2008 | |
Lecture Notes 21
A round of the simplified Feige-Fiat-Shamir protocol is an example of a so-called zero-knowledge interactive proof. We now consider zero knowledge proofs in greater detail.
The secret cave protocol illustrates the fundamental ideas behind zero knowledge without any reference to number theory or hardness of computation. Image a cave with tunnels and doors as shown in Figure 96.1. There are three opening to the cave: L, C, and R. L and R are blocked by exit doors, like at a movie theater, which can be opened from the inside but are locked from the outside. The only way into the cave is through passage C.
The cave itself consists of a U-shaped tunnel that runs between L and R. There is a locked door D in the middle of this tunnel, dividing it into a left part and a right part. There is also a short tunnel from C that leads to a pair of doors DL and DR that lead into the left and right parts of the cave respectively. These doors are also one-way doors that allow passage from C into either the left or right parts of the cave, but once one passes through, the door locks behind and one cannot return to C.
Now, Alice approaches Bob, tells him that she has a key that opens door D, and offers to sell it to him. Bob would really like such a key, as he often goes into the cave to collect mushrooms and would like easy access to both sides of the cave without having to return to the surface to get into the other side. However, he doesn’t trust Alice that the key really works. He tells her, “Give me the key so I can go down into the cave and try it to make sure that it really works.” Alice retorts, “I’m not that dumb. If I give you the key and you disappear into the cave, I’ll probably never see either you or my key again. Pay me first and then try the key.” Bob answers, “If I do that, then you’ll disappear with my money, and I’m likely to be stuck with a non-working key.”
They think about this problem for awhile, and then Alice suggests, “Here’s an idea: I’ll enter the cave through door C, go into the left part of the cave, open D with my key, go through it into the right part of the cave, and then come out door R. When you see me come out R, you’ll know I’ve succeeded in opening the door.” Bob thinks about this and then asks, “How do I know you’ll go into the left part of the cave? Maybe you’ll just go into the right part and come out door R and never go through D.” Alice says, “OK. I’ll go into either the left or right side of the cave. You’ll know I’m there because you’ll hear door DL or DR clank when it closes behind me. You then yell down into the cave which door you want me to come out—L or R—and I’ll do so. If I’m on the opposite side from what you request, then I’ll have no choice but to unlock D in order to pass through to the other side.” Bob is beginning to be satisfied, but he hesitates. “Well, yes, that’s true, but if you’re lucky and happen to be on the side I call out, then you don’t have to use your key at all, and I still won’t know that it works.” Alice answers, “Well, I might be lucky once, but I surely won’t be lucky 20 times in a row, so I’ll agree to do this 20 times. If I succeed in coming out the side you request all 20 times, do you agree to buy my key?” Bob agrees, and they spend the rest of the afternoon climbing in and out of the cave and shouting.
Two undirected graphs G and H are said to be isomorphic if there exists a bijection π from vertices of G to vertices of H that preserves edges. That is, {x,y} is an edge of G if and only if {π(x),π(y)} is an edge of H. There is no polynomial time algorithm known to decide, given two graphs G and H, whether they are isomorphic, also this problem is also not known to be NP-hard. There is also no known polynomial time algorithm for finding the isomorphism π given two isomorphic graphs G and H.
Now, suppose G0 and G1 are public graphs and Alice knows an isomorphism π : G0 → G1. There is a zero knowledge proof whereby Alice can convince Bob that she knows an isomorphism π from G0 to G1, without revealing any information about π. In particular, she can convince Bob in this way that the graphs really are isomorphic, but Bob cannot turn around and convince Carol of that fact.
The protocol is similar to the simplified Feige-Fiat-Shamir protocol and is given in Figure 96.2. If both Alice and Bob follow this protocol, Bob’s check always succeeds. When b = 0, Alice send τ in step 3, and Bob checks that τ is an isomorphism from G0 to H. When b = 1, the function σ that Alice computes is an isomorphism from G1 to H. This is because π-1 is an isomorphism from G1 to G0 and τ is an isomorphism from G0 to H. Composing them gives an isomorphism from G1 to H, so again Bob’s check succeeds.
The protocol is zero knowledge (at least informally) because in both cases, all Bob learns is a random isomorphic copy H of either G0 or G1 and the corresponding isomorphism, information that he could have constructed himself without consulting Alice. What convinces him that Alice really knows π is that in order to repeatedly pass his checks, the graph H of step 1 must be isomorphic to both G0 and G1. Moreover, Alice know isomorphisms σ0 : G0 → H and σ1 : G1 → H since she can produce them upon demand. Hence, she also knows an isomorphism π from G0 to G1, since σ1-1 ∘ σ0 is such a function.
We have seen two examples of zero knowledge interactive proofs of knowledge of a secret. In the simplified Feige-Fiat-Shamir authentication scheme, Alice’s secret is a square root of v. In the graph isomorphism protocol, her secret is the isomorphism π. In all cases, the protocol has the form that Alice sends Bob a “commitment” string x, Bob sends a query bit b, and Alice replies with a response yb. Bob then checks the triple (x,b,yb) for validity.
These protocols both have the property that neither triple (x,0,y0) nor (x,1,y1) alone give any information about Alice’s secret, but y0 and y1 can be combined to reveal her secret. In the FFS protocol, y1y0-1 mod n is a square root of v-1. (Note: Since v-1 has four square roots, the revealed square root might not be the same as Alice’s secret, but it is equally valid as a means of impersonating Alice.) In the graph isomorphism protocol, σ1-1 ∘ σ0 is an isomorphism mapping G0 to G1.
One way to view these protocols is that Alice splits her secret into two parts, y0 and y1. The probabilistic algorithm exemplified by the secret cave protocol allows Alice to convince Bob that she really has (or could produce on demand) both parts, but in doing so, she is only forced to reveal one of them. Each part by itself is statistically independent of the secret and hence gives Bob no information about the secret. Together, they can be used to recover the secret.
This is an example of secret splitting or secret sharing, an important topic in its own right that we will look at later in the term. We have seen other examples of secret sharing already in this course. In the one-time pad cryptosystem, the message m and key k are the same length. Assuming k is picked randomly, then both k and the ciphertext m ⊕ k are random bit strings, which is why Eve learns nothing about m if she doesn’t also possess k. Bob on the other hand recovers m from k and c by computing c ⊕ k. What’s different in the zero knowledge proof example is that Bob has a way to check the validity of the parts that he gets during the protocol.
Not all interactive proofs follow this simple (x,b,y) pattern.
Suppose Alice wants to prove to Bob that G0 and G1 are non-isomorphic graphs. Even ignoring questions of Alice’s privacy, there is no obvious data that she can send Bob that will allow him to easily verify that the two graphs are not isomorphic. However, under a different set of assumptions, Alice can nevertheless convince Bob of that fact, even though Bob couldn’t do so by himself.
In this version of interactive proof, we assume that Alice is all-powerful and can compute
intractable problems. In particular, given two graphs, she can determine whether or not they are
isomorphic. Bob on the other hand has no extraordinary powers and can just perform computation in
the usual way. The way the protocol works is that Alice uses her computational powers to
distinguish isomorphic copies of G0 from isomorphic copies of G1. If G0 G1, there is no
way she could do this, since any graph H isomorphic to one of them is also isomorphic to the
other. So by convincing Bob that she is able to reliably distinguish such graphs, she is, as a
byproduct, also convincing him of the underlying fact that G0 ⁄
G1, there is no
way she could do this, since any graph H isomorphic to one of them is also isomorphic to the
other. So by convincing Bob that she is able to reliably distinguish such graphs, she is, as a
byproduct, also convincing him of the underlying fact that G0 ⁄ G1. The protocol is given in
Figure 97.1.
G1. The protocol is given in
Figure 97.1.
|
|
Note that in this protocol, Alice performs a computation for Bob that he could not do himself. Namely, Alice willingly tells Bob for any H of his choosing whether it is isomorphic to G0 or to G1. (In any implementation of the protocol, she also probably tells him if H is not isomorphic to either one, perhaps by failing in step 2 when b′ is undefined.)
Bit commitment This protocol is also an example of bit-commitment, another important cryptographic primitive that we will study later. A bit-commitment is a kind of encryption of a bit that has the special property that the bit is hidden from anyone not knowing the secret key, and moreover, there is only one valid way of decrypting it. In other words, if c = Ek(b), not only is it impossible, given c to determine whether b = 0 or b = 1, but also, Dk′(c) = b for every k′ for which Dk′(c) is a valid decryption. In other words, if Bob produces a commitment c to a bit b, then b cannot be recovered from c without knowing Bob’s secret encoding key k, but also, there is no key k′ that Bob might release that would make it appear that c is a commitment of the bit 1 - b.
In this interactive proof, H is a commitment of Bob’s bit b. Bob could give H to Carol (who doesn’t
have Alice’s extraordinary computational powers). Later Bob could convince Carol of his bit by telling her
the isomorphism that proves H Gb. But there is nothing he could do to make her believe that his bit was
really 1 - b since H ⁄
Gb. But there is nothing he could do to make her believe that his bit was
really 1 - b since H ⁄ G1-b.
G1-b.
The actual protocol doesn’t use the commitment in quite this way, for rather than Bob later revealing his bit, Alice uses her special powers to discover the bit committed by H. I only point out the relationship to bit commitment now because will be looking at bit commitment later.
We have seen several examples of zero knowledge proofs but no careful definition of what it means to be “zero knowledge”. The intuition that “Bob learns nothing from Alice” surely isn’t true. After running the FFS protocol, for example, Bob learns the quadratic residue x that Alice computed in the first step. He didn’t know x before, nor did he and Alice know any quadratic residues in common other than the public number v. What we do want to capture by the notion of zero knowledge is that Bob learns nothing that might be useful in turning an intractable computation into a tractable one. To that end, we look at arbitrary algorithms for performing computations.
Suppose Mallory is trying to compute some function f(z). We regard Mallory as a probabilistic Turing machine with input tape and output tape. z is placed on the input tape at the beginning. If Mallory halts, the answer is the string that appears on the output tape.
Mallory also has the capability of playing Bob’s role in some zero-knowledge protocol, say FFS for definiteness. This means that during the computation, Mallory can read the number x that Alice sends at the start of FFS. Later, he can send a bit b to Alice. Later still, he can read the response y from Alice. After that, he continues to compute in order to produce the answer, f(z).
A Mallory-simulator, whom we’ll call Sam, is a program like Mallory except he is not on the internet and can’t talk to Alice. Alice’s protocol is zero knowledge if no matter what Mallory one looks at, there is a Mallory-simulator Sam that computes the same random function f(z) as Mallory. In other words, whatever Mallory does with the help of Alice, Sam can do alone. Thus, if Mallory computes some function with Alice’s help (such as writing a square root of v to the output tape), then Sam can also do that without Alice’s help. But under the assumption that taking square roots is hard, Sam couldn’t do that; hence Mallory also couldn’t do that, even after talking with Alice. We conclude that Alice doesn’t release information that would help Mallory to compute her secret; hence her secret is secure.
To show a particular interactive protocol is zero knowledge, it is necessary to show how the simulator can be constructed for an arbitrary program Mallory. Here’s a sketch of how to do that for the FFS protocol.
Sam can generate valid random triples of the form (x,0,y) and random triples of the form (x,1,y) that satisfy Bob’s checking equation x = y2vb mod n. He generates the first kind the same way Alice does—by taking x = r2 mod n and y = r mod n. He generates the second kind by choosing y at random and x = y2v mod n. What he can’t do (without knowing Alice’s secret) is to generate both triples for the same value x. Figure 98.1 sketches how he can simulate Mallory:
|
|
It can be shown that the probability that b = 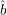 in step 5 is 1/2; hence, the expected number
of times Sam executes lines 1–4 is only 2. It can also be shown that Sam outputs the same
answers as Mallory with the same probability distribution. Hence, the FFS protocol is zero
knowledge.
in step 5 is 1/2; hence, the expected number
of times Sam executes lines 1–4 is only 2. It can also be shown that Sam outputs the same
answers as Mallory with the same probability distribution. Hence, the FFS protocol is zero
knowledge.
Note that this proof depends on Sam’s ability to generate triples of both kinds without knowing Alice’s secret.
One round of the simplified FFS protocol has probability 0.5 of error. That is, Mallory could fool Bob half the time. This is unacceptably high for most applications. By repeating the protocol t times, we reduce this error probability to 1∕2t. Taking t = 20, for example, reduces the probability of error to less than on in a million. The downside of such serial repetition is that it also requires t round trip messages between Alice and Bob (plus a final message from Alice to Bob).
One could also imagine running the t executions of the protocol in parallel. Let (xi,bi,yi) be the messages exchanged during the ith execution of the simplified FFS protocol, 1 ≤ i ≤ t. In a protocol execution, Alice sends (x1,…,xt) to Bob, then Bob sends (b1,…,bt) to Alice, then Alice sends (y1,…,yt) to Bob, and finally Bob checks the t sets of values he has received, accepting only if all checks pass.
A parallel execution is certainly attractive in practice, for it reduces the number of round-trip
messages between Alice and Bob to only 1 1/2. The downside is that the resulting protocol
may not be zero knowledge by our definition. Intuitively, the important difference between the
serial and parallel versions of the protocol is that in the latter, Bob gets to know all of the xi’s
before choosing the bi’s. While it seems implausible that this would actually help a cheating
Bob to compromise Alice secret, the simulation proof used to show that a protocol is zero
knowledge no longer works. First Sam would have to guess (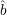 1,…
1,…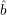 t). Then he can construct the xi’s
and yi’s as before. But when he finally gets to the point in Mallory’s program that Mallory
generates the bi’s, the chance is very high that his initial guesses were wrong and he will be
forced to start over again. Indeed, the probability that all t initial guesses are correct is only
1∕2t.
t). Then he can construct the xi’s
and yi’s as before. But when he finally gets to the point in Mallory’s program that Mallory
generates the bi’s, the chance is very high that his initial guesses were wrong and he will be
forced to start over again. Indeed, the probability that all t initial guesses are correct is only
1∕2t.
The full Feige-Fiat-Shamir Authentication Protocol combines ideas of serial and parallel execution to get a protocol that exhibits some of the properties of both.
A Blum prime is a prime p such that p ≡ 3 (mod 4). A Blum integer is a number n = pq, were p and q are both Blum primes. A special property of Blum integers is that if a is a quadratic residue modulo n, then exactly one of a’s four square roots modulo n is itself a quadratic residue.
To see this, note that a is a quadratic residue modulo both p and q. Claim 4, section 65, of lecture notes 15, shows that one of a’s two square roots is a quadratic residue modulo p, say bp. Then -bp is not a quadratic residue since -1 is not a quadratic residue modulo the Blum prime p by the Euler Criterion of lecture notes 15, section 64. Similar, exactly one of a’s two square roots modulo q is a quadratic residue. Applying the Chinese Remainder Theorem, it follows that exactly one of a’s four square roots modulo n is a quadratic residue.
To generate the public and private keys of the full FFS protocol, Alice chooses a Blum integer n. Next
she chooses random numbers s1,…,sk  Z*
n and random bits c1,…,ck
Z*
n and random bits c1,…,ck  {0,1}. From these, she computes
vi = (-1)cisi-2 mod n, for i = 1,…,k. She makes (n,v1,…,vk) public and keeps (n,s1,…,sk)
private.
{0,1}. From these, she computes
vi = (-1)cisi-2 mod n, for i = 1,…,k. She makes (n,v1,…,vk) public and keeps (n,s1,…,sk)
private.
Notice that every vi is either a quadratic residue or the negation of a quadratic residue. It is easily shown that all of the vi have Jacobi symbol 1 modulo n. A round of the protocol itself is shown in Figure 101.1. The protocol is repeated for a total of t rounds.
|
|
To see that the protocol works when both Alice and Bob are honest, one needs to verify that Bob’s checks will succeed. Plugging in for y, we get that
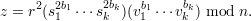
Since vi = (-1)cisk-2, it follows that si2vi = (-1)ci. Hence,
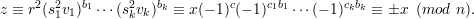
Moreover, since x≠0, then also z≠0. Hence, Bob’s checks succeed.
The chance that a bad Alice can fool Bob is only 1∕2kt. The authors recommend k = 5 and t = 4 for a failure probability of 1∕220.
We have seen that going from a serial composition of interactive proofs to a parallel version reduces communication overhead but possibly at the sacrifice of zero knowledge. Rather surprisingly, one can go a step further to eliminate the interaction from interactive proofs altogether.
The idea here is that Alice will provide Bob with a trace of an execution of herself in an interactive protocol with Bob. Bob will check the trace to make sure that it is a possible record of an interaction between the two of them when both are following the protocol. Of course, that isn’t enough to convince Bob that Alice isn’t cheating, for how does he ensure that Alice simulates random query bits bi for him, and how does he ensure that Alice chooses her xi’s before knowing the bi’s?
The solution to both of these puzzles is to make the bi’s depend in an unpredictable way on the xi’s. We
do this by choosing the bi’s from the value of a hash function applied to the concatenation of the xi’s.
Here’s how it works in, say, the parallel composition of t copies of the simplified FFS protocol. The honest
Alice chooses x1,…,xt according to the protocol. Next she chooses b1…bt to be the first t bits of
H(x1 xt). Finally, she computes y1,…,yt, again according to the protocol. She sends Bob a single
message consisting of x1,…,xt,y1,…,yt. Bob computes b1…bt to be the first t bits of H(x1
xt). Finally, she computes y1,…,yt, again according to the protocol. She sends Bob a single
message consisting of x1,…,xt,y1,…,yt. Bob computes b1…bt to be the first t bits of H(x1 xt) and then
performs each of the t checks of the FFT protocol, accepting Alice’s proof only if all checks
succeed.
xt) and then
performs each of the t checks of the FFT protocol, accepting Alice’s proof only if all checks
succeed.
A cheating Alice can choose yi arbitrarily and then compute a valid xi for a given bi. But if she chooses the bi’s first, the chance that the xi’s she then computes will hash to a string that begins with b1…bt is only 1∕2t.1 If some bi does not agree with the corresponding bit of the hash function, she can either change bi and try to find a new yi that works with the given xi, or she can change xi to try to get the ith bit of the hash value to change. However, neither of these approaches works. The former requires knowledge of Alice’s secret; the latter will cause all of the bits of the hash function to change “randomly”.
Note that one way Alice can attempt to cheat is to use a brute-force attack. For example, she could generate all of the xi’s to be squares of the yi with the hopes that the hash of the xi’s will make all bi = 0. But that is likely to require 2t-1 attempts on average. If t is chosen large enough (say t = 80), the number of trials Alice would have to do in order to have a significant probability of success is prohibitive.
Of course, these observations are not a proof that Alice can’t cheat; only that the obvious strategies don’t work. Nevertheless, it is plausible that a cheating Alice not knowing Alice’s secret, really wouldn’t be able to find a valid such “non-interactive interactive proof”.
Even if this is so, there is an important difference between the true interactive proofs we have been discussing and this kind of non-interactive proof. With a true zero-knowledge interactive proof, Bob does not learn anything about Alice’s secret, nor can Bob impersonate Alice to Carol after Alice has authenticated herself to Bob. On the other hand, if Alice sends Bob a valid non-interactive proof, then Bob can in turn send it on to Carol. Even though Bob couldn’t have produced it on his own, it is still valid. So here we have the curious situation that Alice needs her secret in order to produce the non-interactive proof string π, and Bob can’t learn Alice’s secret from π, but now Bob can use π itself in an attempt to impersonate Alice to Carol.
A signature scheme has a lot in common with the “non-interactive interactive” proofs introduced in section 102. In both cases, there is only a one-way communication from Alice to Bob. Alice signs a message and sends it to Bob. Bob then verifies it without further interaction with Alice. If Bob hands the message to Carol, then Carol can also verify that it was signed by Alice.
Not surprisingly, the “non-interactive interactive proof” ideas can be used to turn the Feige-Fiat-Shamir authentication protocol of section 101 into a signature scheme. The signature scheme we present here is based on a slightly simplified version of the aforementioned protocol in which all of the vi’s in the public key are quadratic residues, and n is not required to be a Blum integer, only a product of two distinct odd primes. The public verification key is (n,v1,…,vk), and the private signing key is (n,s1,…,sk), where vj = sj-2 mod n (1 ≤ j ≤ k).
To sign a message m, Alice simulates t rounds of the protocol in parallel. She first chooses random
r1,…,rt  Zn -{0} and computes
Zn -{0} and computes
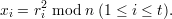
Next she computes u = H(mx1 xt), where H is a suitable cryptographic hash function. She chooses
b1,1,…,bt,k according to the first tk bits of u, that is,
xt), where H is a suitable cryptographic hash function. She chooses
b1,1,…,bt,k according to the first tk bits of u, that is,
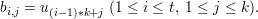
Finally, she computes
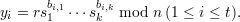
The signature is
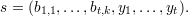
To verify the signed message (m,s), Bob computes
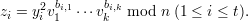
Bob checks that each zi≠0 and that b1,1,…,bt,k are equal to the first tk bits of H(mz1 zt).
zt).
When both Alice and Bob are honest, it is easily verified that zi = xi (1 ≤ i ≤ t). In that case, Bob’s
checks all succeed since xi≠0 and H(mz1 zt) = H(mx1
zt) = H(mx1 xt).
xt).
To forge Alice’s signature, an impostor must find bi,j’s and yi’s that satisfy the equation
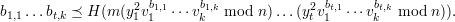
where “≼” means string prefix. It is not obvious how to solve such an equation without knowing a square root of each of the vi-1’s and following essentially Alice’s procedure.