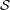 to
a domain of strings
to
a domain of strings 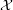 . We will generally find it convenient to assume that all of the seeds in
. We will generally find it convenient to assume that all of the seeds in 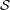 have the
same length n and that all of the strings in
have the
same length n and that all of the strings in 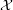 have the same length ℓ, where n ≪ ℓ and ℓ is polynomially
related to n.
have the same length ℓ, where n ≪ ℓ and ℓ is polynomially
related to n.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 22 (rev. 1) | |
| Professor M. J. Fischer | December 1, 2008 | |
Lecture Notes 22
We mentioned cryptographically strong pseudorandom sequence generators in section 31 of lecture notes 7 in connection with stream ciphers. We now explore this topic in greater depth and show how to build one that is provably secure using the same quadratic residuosity assumption that was used in section 67, lecture notes 15, to establish the security of the Goldwasser-Micali probabilistic cryptosystem.
A pseudorandom sequence generator (PRSG) maps a “short” random seed to a “long” pseudorandom bit string. For a PRSG to be cryptographically strong, it must be difficult to correctly predict any generated bit, even knowing all of the other bits of the output sequence. In particular, it must also be difficult to find the seed given the output sequence, since if one knows the seed, then the whole sequence can be generated. Thus, a PRSG is a one-way function and more. While a hash function might generate hash values of the form yy and still be strongly collision-free, such a function could not be a PRSG since it would be possible to predict the second half of the output knowing the first half.
I am being intentionally vague at this stage about what “short” and “long” mean, but intuitively, “short” is a length like we use for cryptographic keys—long enough to prevent brute-force attacks, but generally much shorter than the data we want to deal with. Think of “short”=128 or 256 and you’ll be in the right ballpark. By “long”, we mean much larger sizes, perhaps thousands or even millions of bits, but polynomially related to the seed length. In practice, we usually think of the output length as being variable, so that we can request as many output bits from the generator as we like, and it will deliver them. In this case, “long” refers to the maximum number of bits that can be delivered while still maintaining security. Also, in practice, the bits are generally delivered a block at a time rather than all at once, so we don’t need to announce in advance how many bits we want but can go back as needed to get more.
In a little more detail, a pseudorandom sequence generator G is a function from a domain of seeds 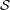 to
a domain of strings
to
a domain of strings 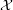 . We will generally find it convenient to assume that all of the seeds in
. We will generally find it convenient to assume that all of the seeds in 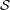 have the
same length n and that all of the strings in
have the
same length n and that all of the strings in 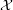 have the same length ℓ, where n ≪ ℓ and ℓ is polynomially
related to n.
have the same length ℓ, where n ≪ ℓ and ℓ is polynomially
related to n.
Intuitively, we want the strings G(s) to “look random”. But what does that mean? Chaitin and Kolmogorov proposed ways of defining what it means for an individual sequence to be considered random. While philosophically very interesting, these notions are somewhat different than the statistical notions that most people mean by randomness and and do not seem to be useful for cryptography.
We take a different tack. We assume that the seeds are chosen truly at random from 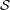 according to the
uniform distribution. Let S be a uniformly distributed random variable over
according to the
uniform distribution. Let S be a uniformly distributed random variable over 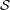 . Then X
. Then X 
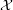 is a derived
random variable defined by X = G(S). For x
is a derived
random variable defined by X = G(S). For x 
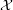 ,
,
![|{s ∈ S | G (s) = x}|
prob[X = x] = ------------------.
|S|](ln220x.png)
Thus, prob[X = x] is the probability of obtaining x as the output of the PRSG for a randomly chosen seed.
We can think of G() as a randomness amplifier. We start with a short truly random seed and obtain a
long string that “looks like” a random string, even though we know it’s not uniformly distributed. In fact, its
distribution is very much non-uniform. Because n ≪ ℓ, |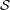 |≤ 2n, and |
|≤ 2n, and |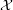 | = 2ℓ, most strings in
| = 2ℓ, most strings in 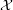 are not
in the range of G and hence have probability 0. For the uniform distribution over
are not
in the range of G and hence have probability 0. For the uniform distribution over 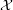 , all strongs have the
same non-zero probability probability 1∕2ℓ.
, all strongs have the
same non-zero probability probability 1∕2ℓ.
More formally, let U be the uniformly distributed random variable over 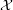 , so prob[U = x] = 1∕2ℓ for
every x
, so prob[U = x] = 1∕2ℓ for
every x 
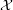 . U is what we usually mean by a “truly random” variable on ℓ-bit strings.
. U is what we usually mean by a “truly random” variable on ℓ-bit strings.
We have already seen that the probability distributions of X = G(S) and U are quite different. Nevertheless, it may be the case that all feasible probabilistic algorithms behave essentially the same whether given a sample chosen according to X or chosen according to U. If that is the case, we say that X and U are algorithmically indistinguishable and that G is a cryptographically strong pseudorandom sequence generator.
Before going further, let me describe some functions G for which G(S) is readily distinguished from U. Suppose every string x = G(s) has the form b1b1b2b2b3b3…, for example 0011111100001100110000…. An algorithm that guesses that x came from G(S) if x is of that form, and guesses that x came from U otherwise, will be right almost all of the time. True, it is possible to get a string of this special form from U, but it is extremely unlikely.
Formally speaking, a judge is a probabilistic Turing machine J that takes an ℓ-bit string as input and
produces a single bit b as output. Because it is probabilistic, it actually defines a random function from 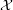 to
{0,1}. This means that for every input x, the output is 1 with some probability px, and the output is 0 with
probability 1 -px. If the input string is itself a random variable X, then the probability that the output is 1
is the weighted sum of px over all possible inputs x, where the weight is the probability prob[X = x]
of input x occurring. Thus, the output value is itself a random variable which we denote by
J(X).
to
{0,1}. This means that for every input x, the output is 1 with some probability px, and the output is 0 with
probability 1 -px. If the input string is itself a random variable X, then the probability that the output is 1
is the weighted sum of px over all possible inputs x, where the weight is the probability prob[X = x]
of input x occurring. Thus, the output value is itself a random variable which we denote by
J(X).
Now, we say that two random variables X and Y are ϵ-indistinguishable by judge J if
![|prob[J(X ) = 1]- prob[J(Y ) = 1]| < ϵ.](ln221x.png)
Intuitively, we say that G is cryptographically strong if G(S) and U are ϵ-indistinguishable for suitably small ϵ by all judges that do not run for too long. A careful mathematical treatment of the concept of indistinguishability must relate the length parameters n and ℓ, the error parameter ϵ, and the allowed running time of the judges, all of which is beyond the scope of this course.
[Note: The topics covered by these lecture notes are presented in more detail and with greater mathematical rigor in handout 17.]
We present a cryptographically strong pseudorandom sequence generator BBS, due to Blum, Blum, and
Shub. BBS is defined by a Blum integer n and an integer ℓ. It maps strings in Z*
n to strings in {0,1}ℓ.
Given a seed s0  Z*n, we define a sequence s1,s2,s3,…,sℓ, where si = si-12 mod n for i = 1,…,ℓ. The
ℓ-bit output sequence BBS(s0) is b1,b2,b3,…,bℓ , where bi = lsb(si).
Z*n, we define a sequence s1,s2,s3,…,sℓ, where si = si-12 mod n for i = 1,…,ℓ. The
ℓ-bit output sequence BBS(s0) is b1,b2,b3,…,bℓ , where bi = lsb(si).
The security of BBS is 0based on the assumed difficulty of determining, for a given a  Z*n with
Jacobi symbol
Z*n with
Jacobi symbol  = 1, whether or not a is a quadratic residue, i.e., whether or not a
= 1, whether or not a is a quadratic residue, i.e., whether or not a  QRn. Recall from
section 67 of lecture notes 15 that this is the same property upon on which the security of the
Goldwasser-Micali probabilistic encryption system relies.
QRn. Recall from
section 67 of lecture notes 15 that this is the same property upon on which the security of the
Goldwasser-Micali probabilistic encryption system relies.
Blum integers were introduced in section 101 of lecture notes 21. Recall that a Blum prime is a prime
p such p ≡ 3 (mod 4), and a Blum integer is a number n = pq, where p and q are distinct Blum primes.
Blum primes and Blum integers have the important property that every quadratic residue a has exactly
one square root y which is itself a quadratic residue. We call such a y the principal square
root of a and denote it by 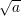 (mod n) or simply by
(mod n) or simply by 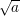 when it is clear that (mod n) is
intended.
when it is clear that (mod n) is
intended.
We need two other facts about Blum integers n. The first claim is that for Blum integers, a quadratic residue and its negation both have the same Jacobi symbol 1.
Proof: This follows from the fact that if a is a quadratic residue modulo a Blum prime, then -a is a quadratic non-residue. Hence,
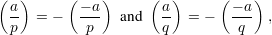
so

__
The second claim simply says that the low-order bits of x mod n and (-x) mod n always differ when n is odd. Let lsb(x) = (x mod 2) be the least significant bit of integer x.
We begin our proof that BBS is cryptographically strong by showing that there is no probabilistic polynomial time algorithm A that, given b2,…,bℓ, is able to predict b1 with accuracy greater than 1∕2 + ϵ. This is not sufficient to establish that the pseudorandom sequence BBS(S) is indistinguishable from the uniform random sequence U, but if it did not hold, there certainly would exist a distinguishing judge. Namely, the judge that outputs 1 if b1 = A(b2,…,bℓ) and 0 otherwise would output 1 with probability greater than 1∕2 + ϵ in the case that the sequence came from BBS(S) and would output 1 with probability exactly 1∕2 in the case that the sequence was truly random.
We now show that if a probabilistic polynomial time algorithm A exists for predicting b1 with accuracy greater than 1∕2 + ϵ, then there is a probabilistic polynomial time algorithm Q for testing quadratic residuosity with the same accuracy. Thus, if quadratic-residue-testing is “hard”, then so is first-bit prediction for BBS.1
Theorem 1 Let A be a first-bit predictor for BBS(S) with accuracy 1∕2 + ϵ. Then we can find an algorithm Q for testing whether a number x with Jacobi symbol 1 is a quadratic residue, and Q will be correct with probability at least 1∕2 + ϵ.
 QRn and 0
to mean x ⁄
QRn and 0
to mean x ⁄ QRn.
QRn. Since  = 1, then either x or -x is a quadratic residue. Let s0 be the principal square root of x or
-x. Let s1,…,sℓ be the state sequence and b1,…,bℓ the corresponding output bits of BBS(s0). We have
two cases.
= 1, then either x or -x is a quadratic residue. Let s0 be the principal square root of x or
-x. Let s1,…,sℓ be the state sequence and b1,…,bℓ the corresponding output bits of BBS(s0). We have
two cases.
Case 1: x  QRn. Then s1 = x, so the state sequence of BBS(s0) is
QRn. Then s1 = x, so the state sequence of BBS(s0) is
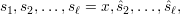
and the corresponding output sequence is
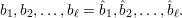
Since 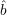 1 = b1, Q(x) correctly outputs 1 whenever A correctly predicts b1. This happens with probability at
least 1∕2 + ϵ.
1 = b1, Q(x) correctly outputs 1 whenever A correctly predicts b1. This happens with probability at
least 1∕2 + ϵ.
Case 2: x  QNRn, so -x
QNRn, so -x  QRn. Then s1 = -x, so the state sequence of BBS(s0) is
QRn. Then s1 = -x, so the state sequence of BBS(s0) is
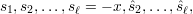
and the corresponding output sequence is
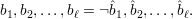
Since 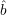 1 = ¬b1, Q(x) correctly outputs 0 whenever A correctly predicts b1. This happens with probability
at least 1∕2 + ϵ.
1 = ¬b1, Q(x) correctly outputs 0 whenever A correctly predicts b1. This happens with probability
at least 1∕2 + ϵ.
In both cases, Q(x) gives the correct output with probability at least 1∕2 + ϵ. __