YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467a: Cryptography and Computer Security | Notes 24 (rev. 1) | |
| Professor M. J. Fischer | December 8, 2008 | |
Lecture Notes 24
The analogy between bit commitment and hash functions described above suggests a bit commitment scheme based on hash functions, as shown in Figure 114.1.
The purpose of r2 is to protect Alice’s secret bit b. To find b before Alice opens the commitment, Bob would have to find r′2 and b′ such that H(r1r′2b′) = c. This is akin to the problem of inverting H and is likely to be hard, although the one-way property for H is not strong enough to imply this. On the one hand, if Bob succeeds in finding such r′2 and b′, he has indeed inverted H, but he does so only with the help of r1—information that is not generally available when attempting to invert H.
The purpose of r1 is to strengthen the protection that Bob gets from the hash properties of H. Even without r1, the strong collision-free property of H would imply that Alice cannot find c, r2, and r′2 such that H(r20) = c = H(r′21). But by using r1, Alice would have to find a new colliding pair for each run of the protocol. This protects Bob by preventing Alice from exploiting a few colliding pairs for H that she might happen to discover.
There are many ways to use a pseudorandom sequence generator G for bit commitment. One such way is shown in Figure 115.1. Here, ρ is a security parameter that controls the probability that a cheating Alice can fool Bob. We let Gρ(s) denote the first ρ bits of G(s).
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Assuming G is cryptographically strong, then c will look random to Bob, regardless of the value of b, so he will be unable to get any information about b.
The purpose of r is to protect Bob against a cheating Alice. Alice can cheat if she can find a triple (c,s0,s1) such that s0 opens c to reveal 0 and s1 opens c to reveal 1. Such a triple must satisfy the following pair of equations:
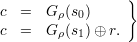 | (1) |
It is sufficient for her to solve the equation
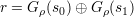 | (2) |
for s0 and s1 and then choose c = Gρ(s0).
One might ask why Bob needs to choose r? Why can’t Alice choose r, or why can’t r be fixed to some constant? If Alice chooses r, then she can easily solve (2) and cheat. If r is fixed to a constant, then if Alice ever finds a triple (c,s0,s1) satisfying (1), she can fool Bob every time. While finding such a pair would be difficult if Gρ were a truly random function, any specific PRSG might have special properties, at least for a few seeds, that would make this possible. For example, suppose r = 1ρ and Gρ(¬s0) = ¬Gρ(s0) for some s0. Then (2) could be solved by taking s1 = ¬s0. By having Bob choose r at random, r will be different each time (with very high probability), and a successful cheating Alice would be forced to solve (1) in general, not just for one special case.
The three bit commitment protocols of the previous section all have the same form. We abstract from these
protocols a cryptographic primitive, called a bit commitment scheme, which consists of a pair of key spaces

 and
and 
 , a blob space
, a blob space  , a commitment function
, a commitment function
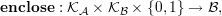
and an opening function
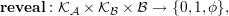
where ϕ means “failure”. We say that a blob c 
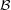 contains b
contains b  {0,1} if reveal(kA,kB,c) = b for some
kA
{0,1} if reveal(kA,kB,c) = b for some
kA 
 A and kB
A and kB 
 B.
B.
These functions have three properties:

 A,∀kB
A,∀kB 
 B,∀b
B,∀b  {0,1}, reveal(kA,kB,enclose(kA,kB,b)) = b;
{0,1}, reveal(kA,kB,enclose(kA,kB,b)) = b;

 B,∀c
B,∀c 
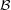 ,∃b
,∃b  {0,1},∀kA
{0,1},∀kA 
 A, reveal(kA,kB,c)
A, reveal(kA,kB,c)  {b,ϕ}.
{b,ϕ}.
The intention is that kA is chosen by Alice and kB by Bob. Intuitively, these conditions say:
A bit commitment scheme looks a lot like a symmetric cryptosystem, with enclose(kA,kB,b) playing the role of the encryption function and reveal(kA,kB,c) the role of the decryption function. However, they differ both in their properties and in the environments in which they are used. Conventional cryptosystems do not require condition 2, nor do they necessarily satisfy it. In a conventional cryptosystem, it is assumed that Alice and Bob trust each other and both share a secret key k. The cryptosystem is designed to protect Alice’s secret message from a passive eavesdropper Eve. In a bit commitment scheme, Alice and Bob cooperate in the protocol but do not trust each other to choose the key. Rather, the key is split into two pieces, kA and kB, with each participant controlling one piece.
A bit commitment scheme can be turned into a bit commitment protocol by plugging it into the generic protocol given in Figure 116.1.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||
The bit commitment protocol of section 113 ((lecture notes 23), and the protocols of sections 114 and 115 above can all be regarded as instances of the generic protocol. For example, we get the protocol of Figure 113.1 (lecture notes 23) by taking
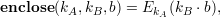
and
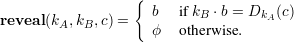
Alice and Bob are in the process of getting divorced and are trying to decide who gets custody of their pet cat, Fluffy. They both want the cat, so they agree to decide by flipping a coin: heads Alice wins; tails Bob wins. Bob has already moved out and does not wish to be in the same room with Alice. The feeling is mutual, so Alice proposes that she flip the coin and telephone Bob with the result.
This proposal of course is not acceptable to Bob since he has no way of knowing whether Alice is telling the truth when she says that the coin landed heads. “Look Alice,” he says, “to be fair, we both have to be involved in flipping the coin. We’ll each flip a private coin and XOR our two coins together to determine who gets Fluffy. You should be happy with this arrangement since even if you don’t trust me to flip fairly, your own fair coin is sufficient to ensure that the XOR is unbiased.” This sounds reasonable to Alice, so she lets him go on to propose the protocol of Figure 117.1. In this protocol, 1 means “heads” and 0 means “tails”.
|
|
After Alice considers Figure 117.1 for awhile, she objects. “This isn’t fair. You get to see my coin flip before I see yours, so now you have complete control over the value of b.” She suggests that she would be happy if the first two steps were reversed, so that Bob flipped his coin first, but Bob balks at that suggestion.
They then both remember last week’s lecture and decide to use blobs to prevent either party from controlling the outcome. They agree on the protocol of Figure 117.2. At the completion of step 2, both Alice and Bob have each other’s commitment (something they failed to achieve in the past, which is why they’re in the middle of a divorce now), but neither know the other’s private bit. They each learn each other’s bit at the completion of steps 3 and 4.
|
|
While this protocol appears to be completely symmetric, it really isn’t quite, for one of the parties completes step 3 before the other one does. Say Alice receives sB before sending sA. At that point, she can compute bB and hence know the coin outcome b. If it turns out that she lost, she might decide to stop the protocol and refuse to complete her part of step 3.
We haven’t really addressed the question for any of these protocols about what happens if one party quits in the middle or one party detects the other party cheating. We have only been concerned until now with the possibility of undetected cheating. But in any real situation, one party might feel that he or she stands to gain by cheating, even if the cheating is detected. That in turn raises complicated questions as to what happens next. Does a third party Carol become involved? If so, can Bob prove to Carol that Alice cheated? What if Alice refuses to talk to Carol? It may be instructive to think about the recourse that Bob has in similar real-life situations and to consider the reasons why such situations rarely arise. For example, what happens if someone fails to follow the provisions of a contract or if someone ignores a summons to appear in court?
There is another subtle problem with the protocol of Figure 117.2. Suppose that Bob sends his message before Alice sends hers in each of steps 1, 2, and 3. Then Alice can choose kA = kB, cA = cB, and sA = sB rather than following her proper protocol. In step 4, Bob will compute
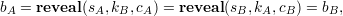
so he won’t detect that anything is wrong, and the coin outcome is b = bA ⊕ bB = bA ⊕ bA = 0. Hence, Alice can force the outcome to be 0 simply by playing copycat.
This problem is not so easy to overcome. One possibility is for both Alice and Bob to check after step 1 that kA≠kB. That way, if Alice, say, plays copycat on steps 2 and 3, there is a good chance that
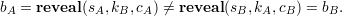
However, depending on the bit commitment scheme, a difference in only one bit in kA and kB might not be enough to ensure that different bits are revealed.
A better idea might be to both check that kA≠kB after step 1 and then to use h(kA) and h(kB) in place of kA and kB, respectively, in the remainder of the protocol, where h is a hash function. That way, even a single bit difference in kA and kB is likely to be magnified to a large difference in the strings h(kA) and h(kB). This should lead to the bits reveal(sA,h(kB),cA) and reveal(sB,h(kA),cB) being uncorrelated, even if sA = sB and cA = cB.
Protocols for coin flipping and for dealing a poker hand from a deck of cards can be based on the intuitive notion of locked boxes. This idea in turn can be implemented using commutative cryptosystems.
We discussed the coin-flipping problem in section 117 and presented a protocol based on bit commitment. Here we present a coin-flipping protocol based on the idea of locked boxes.
Alice and Bob can carry out this protocol electronically using any commutative cryptosystem, that is, one in which EA(EB(m)) = EB(EA(m)) for all messages m. RSA is commutative for keys with a common modulus n, so we can use RSA in an unconventional way. Rather than making the encryption exponent public and keeping the factorization of n private, we turn things around. Alice and Bob jointly chose primes p and q, and both compute n = pq. Alice then chooses an RSA key pair A = ((eA,n),(dA,n)), which she can do since she knows the factorization of n. Similarly, Bob chooses an RSA key pair B = ((eB,n),(dB,n)) using the same n. Alice and Bob both keep their key pairs private (until the end of the protocol, when they reveal them to each other to verify that there was no cheating).
We note that this scheme may have completely different security properties from usual RSA. In RSA, there are three different secrets involved with the key: the factorization of n, the encryption exponent e, and the decryption exponent d. We have seen previously that knowing n and any two of these pieces of information allows the third to be reconstructed. Thus, knowing the factorization of n and e lets one compute d (easy). We also showed in section 56.3 ((lecture notes 13) how to factor n given both e and d.
The way RSA is usually used, only e is public, and it is believed to be hard to find the other quantities. Here we propose making the factorization of n public but keeping e and d private. It may indeed be hard to find e and d, even knowing the factorization of n, but if it is, that fact is not going to follow from the difficulty of factoring n. Of course, for security, we need more than just that it is hard to find e and d. We also need it to be hard to find m given c = me mod n. This is reminiscent of the discrete log problem, but of course n is not prime in this case.
Assuming RSA used in this new way is secure, we can implement the locked box protocol as shown in Figure 118.1. Here we assume that Alice and Bob initially know large primes p and q. In step (2), Alice chooses a random number r such that r < (n - 1)∕2. This ensures that m0 and m1 are both in Zn. Note that i and r can be efficiently recovered from mi since i is just the low-order bit of mi and r = (mi - i)∕2.
|
|
To see that the protocol works when both Alice and Bob are honest, observe that in step 3, cab = EB(EA(mj)) for some j. Then in step 4, cb = DA(EB(EA(mj))) = EB(mj) by the commutativity of EA and EB. Hence, in step 5, m = mj is one of Alice’s strings from step 2.
A dishonest Bob can control the outcome of the coin toss if he can find two keys B and B′ such that EB(ca) = EB′(c′a), where C = {ca,c′a} is the set received from Alice in step 2. In this case, cab = EB(EA(mj)) = EB′(EA(m1-j)) for some j. Then in step 4, cb = EB(mj) = EB′(m1-j). Hence, mj = DB(cb) and m1-j = DB′(cb), so Bob can obtain both of Alice’s messages and then send B or B′ in step 5 to force the outcome to be as he pleases.
The same locked box paradigm can be used for dealing a 5-card poker hand from a deck of cards. Alice takes a deck of cards, places each card in a separate box, and locks each box with her lock. She arranges the boxes in random order and ships them off to Bob. Bob picks five boxes, locks each with his lock, and send them back. Alice removes her locks from those five boxes and returns them to Bob. Bob unlocks them and obtains the five cards of his poker hand. Further details are left to the reader.
In the locked box coin-flipping protocol, Alice has two messages m0 and m1. Bob gets one of them. Alice doesn’t know which (until Bob tells her). Bob can’t cheat to get both messages. Alice can’t cheat to learn which message Bob got. The oblivious transfer problem abstracts these properties from particular applications such as coin flipping and card dealing,
Alice has a secret s. In an oblivious transfer protocol, half of the time Bob learns s and half of the time he learns nothing. Afterwards, Alice doesn’t know whether or not Bob learned s. Bob can do nothing to increase his chances of getting s, and Alice can do nothing to learn whether or not Bob got her secret. Rabin proposed an oblivious transfer protocol based on quadratic residuosity, shown in Figure 119.1, in the early 1980’s.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Alice can can carry out step 3 since she knows the factorization of n and can find all of the square roots of a. However, she has no idea which x Bob used to generate a. Hence, with probability 1∕2, y ≡±x (mod n) and with probability 1∕2, y ⁄≡±x (mod n). If y ⁄≡±x (mod n), then the two factors of n are gcd(x - y,n) and n∕gcd(x - y,n), so Bob factors n and decrypts c in step 4. However, if y ≡±x (mod n), he learns nothing, and Alice’s secret is as secure as RSA itself.
There is one potential problem with this protocol. A cheating Bob in step 2 might send a number a which he generated by some other means than squaring a random x. In this case, he learns something new no matter which square root Alice sends him in step 3. Perhaps that information, together with what he already learned in the course of generating a, is enough for him to factor n. We don’t know of any method by which Bob could find a quadratic residue without also knowing one of its square roots. We certainly don’t know of any method that would produce a quadratic residue a and some other information Ξ that, combined with y, would allow Bob to factor n. But we also cannot prove that no such method exists.
We can fix this protocol by inserting between steps 2 and 3 a zero knowledge proof that Bob knows a square root of a. This is essentially what the simplified Feige-Fiat-Shamir protocol does, but we have to reverse the roles of Alice and Bob. Now Bob is the one with the secret square root x. He wants to prove to Alice that he knows x, but he does not want Alice to get any information about x, since if she learns x, she could choose y = x and reduce his chances of learning s while still appear to be playing honestly. Again, details are left to the reader.
In the one-of-two oblivious transfer, Alice has two secrets, s0 and s1. Bob always gets exactly one of the secrets. He gets each with probability 1/2, and Alice does not know which he got.
The locked box protocol is one way to implement one-of-two oblivious transfer. Another is based on a public key cryptosystem (such as RSA) and a symmetric cryptosystem (such as AES). This protocol, given in Figure 119.2, does not rely on the cryptosystems being commutative.
|
|
In step 2, Bob encrypts a randomly chosen key k for the symmetric cryptosystem using one of the PKS encryption keys that Alice sent him in step 1. In step 2, Bob selects one of the two encryption keys from Alice, uses it to encrypt k, and sends the encryption to Alice. In step 3, Alice decrypts c using both decryption keys d0 and d1 to get k0 and k1. One of the ki is Bob’s key k (kb to be specific) and the other is garbage, but because k is random and she doesn’t know b, she can’t tell which is k. She then encrypts one secret with k0 and the other with k1, using the random bit b′ to ensure that each secret is equally likely to be encrypted by the key that Bob knows. In step 4, Bob decrypts the ciphertext cb using key his key k = kb to recover the secret s = sb⊕b′. He can’t decrypt the other ciphertext c1⊕b since he doesn’t know the key k1⊕b used to produce it, nor does he know the decryption key d1⊕b that would allow him to find it from c.