Let a ≥ 0, n Z+. Let QR(a,n) hold if (a,n) = 1 and a is a quadratic residue modulo n. Let QNR(a,n) hold if (a,n) = 1 and a is a quadratic non-residue modulo n (i.e., there is no y Z*_n such that a ≡ y² (mod n)).

For a prime p, the structure of quadratic residues can be fairly easily explained. Let g be a primitive root of Z*_p. Then every element of Z*_p is uniquely expressible as g^k for some k {0,…,p - 2}.

Conversely, suppose a ≡ y² (mod p). Write y ≡ g^ℓ (mod p). Then g^k ≡ g^2ℓ (mod p). Multiplying both sides by g^-k, we have 1 ≡ g⁰ ≡ g^2ℓ-k (mod p). But then ϕ(p)∣2ℓ - k. Since 2∣ϕ(p) = p - 1, it follows that 2∣k, as desired. __

The following theorem, due to Euler, is now easily proved:

Theorem 2 (Euler) Let p be an odd prime, and let a ≥ 0, (a,p) = 1. Then

If QR(a,p) holds, then a is a quadratic residue modulo p, so k is even by Theorem 1. Write k = 2r for some r. Then a^(p-1)∕2 ≡ g^2r(p-1)∕2 ≡ (g^r)^p-1 ≡ 1 (mod p) by Fermat’s theorem.

If QNR(a,p) holds, then a is a quadratic non-residue modulo p, so k is odd by Theorem 1. Write k = 2r + 1 for some r. Then a^(p-1)∕2 ≡ g^{(2r+1)(p-1)∕2} ≡ g^r(p-1)g^(p-1)∕2 ≡ g^(p-1)∕2 (mod p). Let b = g^(p-1)∕2. Clearly b² ≡ 1 (mod p), so b ≡ ±1 (mod p).¹ Since g is a primitive root modulo p and (p - 1)∕2 < p - 1, b = g^(p-1)∕2 ⁄≡ 1 (mod p). Hence, b ≡-1 (mod p). __ Definition: The Legendre symbol is a function of two integers a and p, written 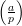. It is defined for a ≥ 0 and p an odd prime as follows:

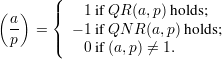
A multiplicative property of the Legendre symbols follows immediately from Theorem 1.

Observation 3 Let a,b ≥ 0, p an odd prime. Then

As an easy corollary of Theorem 2, we have:

Corollary 4 Let a ≥ 0 and let p be an odd prime. Then

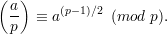
The Jacobi symbol extends the domain of the Legendre symbol. Definition: The Jacobi symbol is a function of two integers a and n, written , that is defined for all a ≥ 0 and all odd positive integers n. Let ∏ _i=1^kp_i^e_i be the prime factorization of n. Then

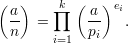
Here denotes the previously-defined Legendre symbol. (Note that by this definition, 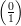= 1, and = 0 for odd n ≥ 3.)

We have seen that if (a,p) = 1 and p is prime, then the Legendre symbol = 1 iff a is a quadratic residue modulo p. It is not true for the Jacobi symbol that ≡ 1 (mod n) implies that a is a quadratic residue modulo n. For example, 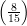= 1, but 8 is not a quadratic residue modulo 15. However, the converse does hold:

The usefulness of the Jacobi symbol stems from its ability to be computed efficiently, even without knowning the factorization of either a or n. The algorithm is based on the following theorem, which is stated without proof.

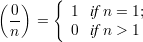
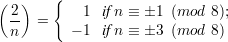
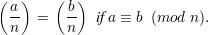
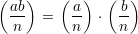
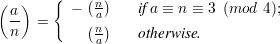
Theorem 6 leads directly to a recursive algorithm for computing :