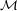 =
= 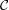 = {0,1,2,3}, where the joint probability distribution
over message-ciphertext pairs is described by the table below.
= {0,1,2,3}, where the joint probability distribution
over message-ciphertext pairs is described by the table below.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #10 | |
| Xueyuan Su | March 1, 2010 | |
Solution to Midterm Examination
This is a closed book examination. Answer any 5 of the following 6 questions. Write the numbers of the five questions that you want graded on the cover of your bluebook. All questions count equally. You have 75 minutes. Remember to write your name on your bluebook and to justify your answers. Good Luck!
___________________________________________________________________________________
Consider a symmetric cryptosystem with 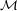 =
= 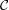 = {0,1,2,3}, where the joint probability distribution
over message-ciphertext pairs is described by the table below.
= {0,1,2,3}, where the joint probability distribution
over message-ciphertext pairs is described by the table below.
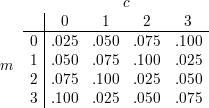
 and an encryption function c = Ek(m) that gives rise to the given
joint probability distribution when keys are chosen uniformly from
and an encryption function c = Ek(m) that gives rise to the given
joint probability distribution when keys are chosen uniformly from  .
.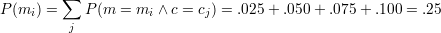
![P-[m--=-0∧-c-=-3] .100-
P [m = 0 | c = 3] = P [c = 3] = .25 = .400](ho102x.png)
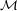 . Namely,
. Namely,
![(
||| .100 if m + c ≡ 0 (mod 4)
{ .200 if m + c ≡ 1 (mod 4)
P [m | c] = || .300 if m + c ≡ 2 (mod 4)
|( .400 if m + c ≡ 3 (mod 4)](ho103x.png)
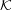 = {0,1,2,3,5,6,7,10,11,15} and
Ek(m) = (k - m) mod 4.
= {0,1,2,3,5,6,7,10,11,15} and
Ek(m) = (k - m) mod 4.Problem 2: Security of a Symmetric Cryptosystem
Happy Hacker decides to improve on the Caesar cipher by making the key space larger. He keeps  =
=
 = {0, …, 25} as before, but he lets
= {0, …, 25} as before, but he lets 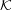 = {0,…,49} and defines
= {0,…,49} and defines
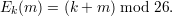
Compare the security of Hacker’s system with the ordinary Caesar cipher. Justify your answers.
Solution: Hacker’s system is less secure than ordinary Caesar, despite the larger key space. Because Ek(m) = Ek mod 26(m) for any k, the larger key space does not increase the number of possible encryption functions, but it does alter their distribution. Now, E0(),…,E23() are twice as likely to be chosen as E24() and E25(), so P[m∣c] is not uniformly distributed, and Eve gets partial information about m from seeing c.
Let 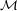 =
= 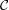 = {0,…,25} as in the Caesar cipher. Let the key space
= {0,…,25} as in the Caesar cipher. Let the key space  be an arbitrary finite set, let
f :
be an arbitrary finite set, let
f : 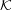 →
→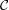 be an arbitrary function, and let Ek(m) = (f(k) + m) mod 26.
be an arbitrary function, and let Ek(m) = (f(k) + m) mod 26.
For each of the following questions, answer whether it holds for all  and f(), for some
and f(), for some  and f(), or
for no
and f(), or
for no  and f().
and f().

 ? If so, define
it. If not, explain why not.
? If so, define
it. If not, explain why not.
Justify your answers.
 and f(). The decryption function is
and f(). The decryption function is
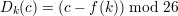
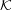 ,f() pairs.
,f() pairs.
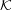 =
= 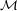 and f() is the identity function, then the resulting
cryptosystem is the ordinary Caeser cipher, which is known to have the group property.
and f() is the identity function, then the resulting
cryptosystem is the ordinary Caeser cipher, which is known to have the group property.

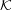 , then the resulting cryptosystem does not
have the group property. Choose k1 = k2
, then the resulting cryptosystem does not
have the group property. Choose k1 = k2 
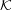 . Then Ek1,k2(m) = Ek2(Ek1(m)) =
(m + 2) mod 26. Since Ek3(m) = (m + 1) mod 26 for all k3
. Then Ek1,k2(m) = Ek2(Ek1(m)) =
(m + 2) mod 26. Since Ek3(m) = (m + 1) mod 26 for all k3 
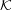 , there is no k3 for
which Ek3 = Ek1,k2; hence, the group property does not hold.
, there is no k3 for
which Ek3 = Ek1,k2; hence, the group property does not hold.DES is built from a Feistel network.
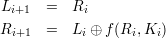
To decrypt a ciphertext (Lt,Rt), each stage works as follows:
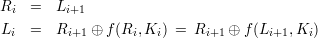
Problem 5: Message Authentication Codes (MAC)
Problem 6: Congruence Equations
 Zn.
Zn.
 Zn iff n∣(ax - b) for some
x
Zn iff n∣(ax - b) for some
x  Z iff
Z iff
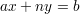
for some x,y  Z. This is a linear Diophantine equation. It has a solution iff gcd(a,n)∣b.
Z. This is a linear Diophantine equation. It has a solution iff gcd(a,n)∣b.
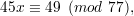 | (1) |
we solve the corresponding Diophantine equation
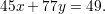 | (2) |
Since gcd(45,77) = 1∣49, this Diophantine equation has a solution. We use the extended Euclidean algorithm to solve it.
| i | ri | ui | vi | qi |
| 1 | 45 | 1 | 0 | |
| 2 | 77 | 0 | 1 | 0 |
| 3 | 45 | 1 | 0 | 1 |
| 4 | 32 | -1 | 1 | 1 |
| 5 | 13 | 2 | -1 | 2 |
| 6 | 6 | -5 | 3 | 2 |
| 7 | 1 | 12 | -7 |
Therefore, x = 12 and y = -7 satisfies
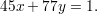 | (3) |
The solution to (2) is x = 12 × 49 = 588 and y = -7 × 49 = -343. The solution to (1) is x mod 77 = 588 mod 77 = 49.
(end of exam)