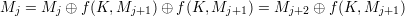
Therefore, given MmMm+1, we compute
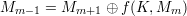
Repeating the same process until M0 is computed. Then M0M1 is the corresponding plaintext.
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #11 | |
| Xueyuan Su | March 3, 2010 | |
Solutions to Problem Set 3
Due on Tuesday, February 23, 2010.
In the problems below, “textbook” refers to Wade Trapp and Lawrence C. Washington, Introduction to Cryptography with Coding Theory, Second Edition, Prentice-Hall, 2006.
Textbook, problem 4-1.
Solution:
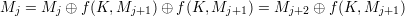
Therefore, given MmMm+1, we compute
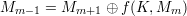
Repeating the same process until M0 is computed. Then M0M1 is the corresponding plaintext.
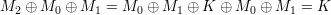
Problem 2: DES Complementation Property
Textbook, problem 4-4.
Solution: Define C = DES(P,K) and C′ = DES(P,K). The heart of DES is the Feistel network, whose one stage algorithm is described by (1) and (2).
For DES(L0R0,K), define L0′ = L0, R0′ = R0 and Ki′ = Ki, which leads to another instance DES(L0′R0′,K′). We will show that for any stage of the Feistel network, Li′ = Li and Ri′ = Ri.
For instance DES(L0R0,K),
For instance DES(L0′R0′,K′), Since f(Ri,Ki) uses the bitwise ⊕ operation to combine input bits of Ri (after expansion) and Ki before the permutation in S-boxes, and ⊕ operation is associative and commutative, the following holds for any r and k of the same length,
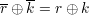 | (7) |
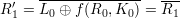 | (8) |
For instance DES(L0R0,K),
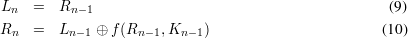
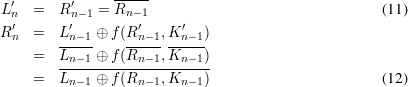
Therefore, after 16 stages of Feistel network, we can get L16′ = L16 and R16′ = R16. Concatenating L16′ and R16′, we conclude
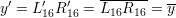 | (13) |
Textbook, problem 4-6.
Solution: This version of Triple DES is vulnerable to a known plaintext attack, similar to Double DES is. Suppose the attacker Eve knows a plaintext-ciphertext pair (m,c). She first computes EK(EK(m)) and DK(c) for all possible K. Then Eve looks for the intersection of these two sets. We know the intersection is not empty since the actual key pair (K1,K2) must work. Then if there is only one matching key pair, Eve immediately knows the correct key pair. If there are more than one matching pairs, Eve can use other known plaintext-ciphertext pairs to further reduce the number of candidate key pairs. Essentially, if we define EK′() = EK(EK()), then the meet-in-the-middle attack can be carried out in exactly the same way as in Double DES.
Problem 4: Modified Feistel Network
Textbook, problem 4-8.
Solution: We prove the correctness of the decryption function by induction.

Therefore, the claim is true for all i. As a result, A0B0C0 is the correct plaintext.
Textbook, problem 4-9. (Note: “CFB mode” as used in this problem is what we called “Extended CFB mode” in the lectures.)
Solution:
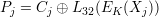
We also update Xj in the same way as
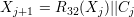
Problem 6: Fast exponentiation algorithm
A recursive algorithm for modular exponentiation was presented in class (Lecture 8, slide 17).
Here is a different recursive algorithm to do the same thing.
Both algorithms operate by computing mk (mod n) for various integers k.
Solution:
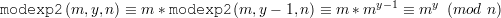
If y is even,
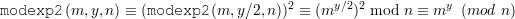
In both cases, modexp2 is correct.