 Ω. We will also regard D as a random variable that ranges over Ω and assumes value ω
Ω. We will also regard D as a random variable that ranges over Ω and assumes value ω  Ω
with probability PD(ω).
Ω
with probability PD(ω).
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #14 | |
| Professor M. J. Fischer | April 6, 2010 | |
Pseudorandom Sequence Generation
Let D be a probability distribution on a finite set Ω. Then D associates a probability PD(ω) with each each
element ω  Ω. We will also regard D as a random variable that ranges over Ω and assumes value ω
Ω. We will also regard D as a random variable that ranges over Ω and assumes value ω  Ω
with probability PD(ω).
Ω
with probability PD(ω).
Definition: An (S,ℓ)-pseudorandom sequence generator (PRSG) is a function f:S → {0,1}ℓ.
(We generally assume 2ℓ ≫ |S|.) More properly speaking, a PRSG is a randomness amplifier.
Given a random, uniformly distributed seed s  S, the PRSG yields the pseudorandom sequence
z = f(s). We use S also to denote the uniform distribution on seeds, and we denote the induced
probability distribution on pseudorandom sequences by f(S).
S, the PRSG yields the pseudorandom sequence
z = f(s). We use S also to denote the uniform distribution on seeds, and we denote the induced
probability distribution on pseudorandom sequences by f(S).
The goal of an (S,ℓ)-PRSG is to generate sequences that “look random”, that is, are computationally indistinguishable from sequences drawn from the uniform distribution U on length-ℓ sequences. Informally, a probabilistic algorithm A that always halts “distinguishes” X from Y if its output distribution is “noticeably differently” depending whether its input is drawn at random from X or from Y . Formally, there are many different kinds of distinguishably. In the following definition, the only aspect of A’s behavior that matters is whether or not it outputs “1”. Definition: Let ϵ > 0, let X, Y be distributions on {0,1}ℓ, and let A be a probabilistic algorithm. Algorithm A naturally induces probability distributions A(X) and A(Y ) on the set of possible outcomes of A. We say that A ϵ-distinguishes X and Y if
![|P [A (X ) = 1]- P [A(Y ) = 1]| ≥ ϵ,](ho140x.png)
and we say X and Y are ϵ-indistinguishable by A if A does not distinguish them.
A natural notion of randomness for PRSG’s is that the next bit should be unpredictable given all of the bits that have been generated so far. Definition: Let ϵ > 0 and 1 ≤ i ≤ ℓ. A probabilistic algorithm Ni is an ϵ-next bit predictor for bit i of f if
![1
P [Ni(Z1,...,Zi-1) = Zi] ≥ -+ ϵ
2](ho141x.png)
where (Z1,…,Zℓ) is distributed according to f(S).
A still stronger notion of randomness for PRSG’s is that each bit i should be unpredictable, even if one is given all of the bits in the sequence except for bit i. Definition: Let ϵ > 0 and 1 ≤ i ≤ ℓ. A probabilistic algorithm Bi is an ϵ-strong bit predictor for bit i of f if
![1
P [Bi(Z1,...,Zi-1,Zi+1,...,Zℓ) = Zi] ≥--+ ϵ
2](ho142x.png)
where (Z1,…,Zℓ) is distributed according to f(S).
The close relationship between distinguishability and the two kinds of bit prediction is established in the following theorems.
Theorem 1 Suppose ϵ > 0 and Ni is an ϵ-next bit predictor for bit i of f. Then algorithm Bi is an ϵ-strong bit predictor for bit i of f, where algorithm Bi(z1,…,zi-1,zi+1,…,zℓ) simply ignores its last ℓ - i inputs and computes Ni(z1,…,zi-1).
Proof: Obvious from the definitions. __
Let  = (x1,…,xℓ) be a vector. We define
= (x1,…,xℓ) be a vector. We define  i to be the result of deleting the ith element of
i to be the result of deleting the ith element of  , that is,
, that is,
 i = (x1,…,xi-1,xi+1,…,xℓ).
i = (x1,…,xi-1,xi+1,…,xℓ).
Theorem 2 Suppose ϵ > 0 and Bi is an ϵ-strong bit predictor for bit i of f. Then algorithm A
ϵ-distinguishes f(S) and U, where algorithm A on input  outputs 1 if Bi(
outputs 1 if Bi( i) = xi and outputs 0
otherwise.
i) = xi and outputs 0
otherwise.
Proof: By definition of A, A( ) = 1 precisely when Bi(
) = 1 precisely when Bi( i) = xi. Hence, P[A(f(S)) = 1] ≥
1∕2 + ϵ. On the other hand, for
i) = xi. Hence, P[A(f(S)) = 1] ≥
1∕2 + ϵ. On the other hand, for  = U, P[Bi(
= U, P[Bi( i) = ri] = 1∕2 since ri is a uniformly distributed
bivalued random variable that is independent of
i) = ri] = 1∕2 since ri is a uniformly distributed
bivalued random variable that is independent of  i. Thus, P[A(U) = 1] = 1∕2, so A ϵ-distinguishes
f(S) and U. __
i. Thus, P[A(U) = 1] = 1∕2, so A ϵ-distinguishes
f(S) and U. __
For the final step in the 3-way equivalence, we have to weaken the error bound.
Theorem 3 Suppose ϵ > 0 and algorithm A ϵ-distinguishes f(S) and U. For each 1 ≤ i ≤ ℓ and
c  {0,1}, define algorithm Nic(z1,…,zi-1) as follows:
{0,1}, define algorithm Nic(z1,…,zi-1) as follows:
| 1. | Flip coins to generate ℓ - i + 1 random bits ri,…,rℓ. |
| 2. | Let v = |
| 3. | Output v ⊕ ri ⊕ c. |
Then there exist m and c for which algorithm Nmc is an ϵ∕ℓ-next bit predictor for bit m of f.
Proof: Let (Z1,…,Zℓ) = f(S) and (R1,…,Rℓ) = U be random variables, and let Di = (Z1,…,Zi,Ri+1,…,Rℓ). Di is the distribution on ℓ-bit sequences that results from choosing the first i bits according to f(S) and choosing the last ℓ-i bits uniformly. Clearly D0 = U and Dℓ = f(S).
Let pi = P[A(Di) = 1], 0 ≤ i ≤ ℓ. Since A ϵ-distinguishes Dℓ and D0, we have |pℓ - p0| ≥ ϵ. Hence, there exists m, 1 ≤ m ≤ ℓ, such that |pm - pm-1| ≥ ϵ∕ℓ. We show that the probability that Nmc correctly predicts bit m for f is 1∕2 + (pm - pm-1) if c = 1 and 1∕2 + (pm-1 - pm) if c = 0. It will follow that either Nm0 or Nm1 correctly predicts bit m with probability 1∕2 + |pm - pm-1|≥ ϵ∕ℓ.
Consider the following experiments. In each, we choose an ℓ-tuple (z1,…,zℓ) according to f(S) and an ℓ-tuple (r1,…,rℓ) according to U.
Let qj be the probability that experiment Ej succeeds, where j = 0,1,2. Clearly q2 = (q0 + q1)∕2 since rm = zm is equally likely as rm = ¬zm.
Now, the inputs to A in experiment E0 are distributed according to Dm, so pm = q0. Also, the inputs to A in experiment E2 are distributed according to Dm-1, so pm-1 = q2. Differencing, we get pm - pm-1 = q0 - q2 = (q0 - q1)∕2.
We now analyze the probability that Nmc correctly predicts bit m of f(S). Assume without loss of generality that A’s output is in {0,1}. A particular run of Nmc(z1,…,zm-1) correctly predicts zm if
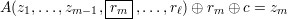 | (1) |
If rm = zm, (1) simplifies to
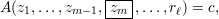 | (2) |
and if rm = ¬zm, (1) simplifies to
 | (3) |
Let OKmc be the event that Nmc(Z1,…,Zm-1) = Zm, i.e., that Nmc correctly predicts bit m for f. From (2), it follows that
![{
c q0 if c = 1
P[OK m | Rm = Zm] = (1 - q0) if c = 0](ho1418x.png)
for in that case the inputs to A are distributed according to experiment E0. Similarly, from (3), it follows that
![{
c q1 if ¬c = 1
P [OK m | Rm = ¬Zm ] = (1 - q1) if ¬c = 0](ho1419x.png)
for in that case the inputs to A are distributed according to experiment E1. Since P[Rm = Zm] = P[Rm = ¬Zm] = 1∕2, we have
![P [OKcm ] = 1-⋅P [OKcm | Rm = Zm ]+ 1-⋅P [OKcm | Rm = ¬Zm ]
2 2
{ q0∕2+ (1- q1)∕2 = 1∕2 + pm - pm- 1 if c = 1
=
q1∕2+ (1- q0)∕2 = 1∕2 + pm- 1 - pm if c = 0.](ho1420x.png)
 {0,1}, as desired. __
{0,1}, as desired. __
We now give a PRSG due to Blum, Blum, and Shub for which the problem distinguishing its outputs from the uniform distribution is closely related to the difficulty of determining whether a number with Jacobi symbol 1 is a quadratic residue modulo a certain kind of composite number called a Blum integer. The latter problem is believed to be computationally hard. First some background.
A Blum prime is a prime number p such that p ≡ 3 (mod 4). A Blum integer is a number n = pq,
where p and q are Blum primes. Blum primes and Blum integers have the important property that every
quadratic residue a has a square root y which is itself a quadratic residue. We call such a y a principal
square root of a and denote it by 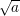 .
.
Lemma 4 Let p be a Blum prime, and let a be a quadratic residue modulo p. Then y = a(p+1)∕4 mod p is a principal square root of a modulo p.
Proof: We must show that, modulo p, y is a square root of a and y is a quadratic residue. By the Euler criterion [Theorem 2, handout 15], since a is a quadratic residue modulo p, we have a(p-1)∕2 ≡ 1 (mod p). Hence, y2 ≡ (a(p+1)∕4)2 ≡ aa(p-1)∕2 ≡ a (mod p), so y is a square root of a modulo p. Applying the Euler criterion now to y, we have
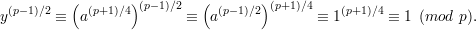
Hence, y is a quadratic residue modulo p. __
Theorem 5 Let n = pq be a Blum integer, and let a be a quadratic residue modulo n. Then a has four square roots modulo n, exactly one of which is a principal square root.
Proof: By Lemma 4, a has a principal square root u modulo p and a principal square root v modulo q. Using the Chinese remainder theorem, we can find x that solves the equations
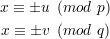
for each of the four choices of signs in the two equations, yielding 4 square roots of a modulo n. It is easily shown that the x that results from the +,+ choice is a quadratic residue modulo n, and the others are not. __
From Theorem 4, it follows that the mapping b b2 mod n is a bijection from the set of quadratic
residues modulo n onto itself. (A bijection is a function that is 1–1 and onto.)
b2 mod n is a bijection from the set of quadratic
residues modulo n onto itself. (A bijection is a function that is 1–1 and onto.)
Definition: The Blum-Blum-Shub generator BBS is defined by a Blum integer n = pq and
an integer ℓ. It is a (Z*
n,ℓ)-PRSG defined as follows: Given a seed s0  Z*n, we define a
sequence s1,s2,s3,…,sℓ, where si = si-12 mod n for i = 1,…,ℓ. The ℓ-bit output sequence is
b1,b2,b3,…,bℓ , where bi = si mod 2.
Z*n, we define a
sequence s1,s2,s3,…,sℓ, where si = si-12 mod n for i = 1,…,ℓ. The ℓ-bit output sequence is
b1,b2,b3,…,bℓ , where bi = si mod 2.
Note that any sm uniquely determines the entire sequence s1,…,sℓ and corresponding output bits.
Clearly, sm determines sm+1 since sm+1 = sm2 mod n. But likewise, sm determines sm-1 since
sm-1 = 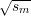 , the principal square root of sm modulo n, which is unique by Theorem 5.
, the principal square root of sm modulo n, which is unique by Theorem 5.
Theorem 6 Suppose there is a probabilistic algorithm A that ϵ-distinguishes BBS(Z*n) from U.
Then there is a probabilistic algorithm Q(x) that correctly determines with probability at least
ϵ′ = ϵ∕ℓ whether or not an input x  Z*n with Jacobi symbol
Z*n with Jacobi symbol  = 1 is a quadratic residue
modulo n.
= 1 is a quadratic residue
modulo n.
Proof: From A, one easily constructs an algorithm  that reverses its input and then applies A.  ϵ-distinguishes the reverse of BBS(Z*n) from U. By Theorem 3, there is an ϵ′-next bit predictor Nm for bit ℓ - m + 1 of BBS reversed. Thus, Nm(bℓ,bℓ-1,…,bm+1) correctly outputs bm with probability at least 1∕2 + ϵ′, where (b1,…,bℓ) is the (unreversed) output from BBS(Z*n).
We now describe algorithm Q(x), assuming x  Z*n and
Z*n and  = 1. Using x as a seed,
compute (b1,…,bℓ) = BBS(x) and let b = Nm(bℓ-m,bℓ-m-1,…,b1). Output “quadratic residue”
if b = x mod 2 and “non-residue” otherwise.
= 1. Using x as a seed,
compute (b1,…,bℓ) = BBS(x) and let b = Nm(bℓ-m,bℓ-m-1,…,b1). Output “quadratic residue”
if b = x mod 2 and “non-residue” otherwise.
To see that this works, observe first that Nm(bℓ-m,bℓ-m-1,…,b1) correctly predicts b0 with
probability at least 1∕2 + ϵ′, where b0 = (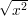 mod n) mod 2. This is because we could in
principle let sm+1 = x2 mod n and then work backwards defining sm =
mod n) mod 2. This is because we could in
principle let sm+1 = x2 mod n and then work backwards defining sm = 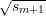 mod n,
sm-1 =
mod n,
sm-1 = 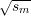 mod n, …, s0 =
mod n, …, s0 = 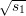 mod n. It follows that b0,…,bℓ-m are the last ℓ - m + 1 bits of
BBS(s0), and b0 is the bit predicted by Nm.
mod n. It follows that b0,…,bℓ-m are the last ℓ - m + 1 bits of
BBS(s0), and b0 is the bit predicted by Nm.
Now, x and -x are clearly square roots of sm+1. We show that they both have Jacobi symbol 1.
Since  =
=  ⋅
⋅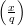 = 1, then either
= 1, then either  =
= 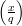 = 1 or
= 1 or  =
= 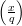 = -1.
But because p and q are Blum primes, -1 is a quadratic non-residue modulo both p and q, so
= -1.
But because p and q are Blum primes, -1 is a quadratic non-residue modulo both p and q, so
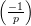 =
= 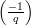 = -1. It follows that
= -1. It follows that 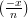 = 1. Hence, x = ±
= 1. Hence, x = ±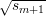 , so exactly one of x and
-x is a quadratic residue.
, so exactly one of x and
-x is a quadratic residue.
Since n is odd, x mod n and -x mod n have opposite parity. Hence, x is a quadratic residue
iff x and 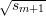 have the same parity. But Nm outputs
have the same parity. But Nm outputs 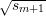 mod 2 with probability 1∕2 + ϵ′,
so it follows that Q correctly determines the quadratic residuosity of its argument with probability
1∕2 + ϵ′. __
mod 2 with probability 1∕2 + ϵ′,
so it follows that Q correctly determines the quadratic residuosity of its argument with probability
1∕2 + ϵ′. __