In the problems below, “textbook” refers to Wade Trapp and Lawrence C. Washington, Introduction to Cryptography with Coding Theory, Second Edition, Prentice-Hall, 2006.

Problem 1: Zero Knowledge

[The following is a modification of Problem 14-3 of the textbook.]

Naive Nelson thinks he understands zero-knowledge protocols. He wants to prove to Victor that he knows the factorization of n (which equals pq for two large distinct primes p and q) without revealing this factorization to Victor or anyone else. Nelson devises the following procedure: Victor chooses a random integer x mod n, computes y = x² mod n, and sends y to Nelson. Nelson computes a square root s of y (mod n) and sends s to Victor. Victor checks that s² ≡ y (mod n). Victor repeats this 20 times.

1. Describe how Nelson computes s. You may assume that p and q are ≡ 3 (mod 4).
2. Describe why successful completion of this protocol convinces Victor that Nelson really does know the factorization of n (subject to a very small probability of error). In particular, show that any feasible algorithm able to satisfy Victor’s queries can be converted into a feasible probabilistic algorithm for printing out the factors of n.
3. Explain how, with high probability of success, Victor can use this protocol to find the factorization of n. (Therefore, this is not a zero-knowledge protocol.)
4. Suppose Eve is eavesdropping and hears the values of each y and s. Is it likely that Eve obtains any useful information? (Assume no value of y repeats.)

Problem 2: Indistinguishability

Happy Hacker wanted a good source of random bits, so he downloaded a cryptographically secure pseudorandom sequence generator G(s) from the Internet. G maps seeds of length n to binary sequences of length ℓ. Knowing the importance of seeding the generator with truly random bits, he arranged to obtain the seed s from /dev/random. Having done so, he couldn’t see any good reason to “waste” the random bits in s, so he decided to output the string s ⋅ G(s), giving n + ℓ output bits in all. In other words, he built a new pseudorandom number generator G′(s) = s ⋅ G(s).

Unfortunately, G′(s) is not cryptographically secure, even when seeded properly with a truly random seed s. Explain why, and describe a judge J that can distinguish the distribution G′(S) from U. Here, S is the uniform distribution over the seed space, and U is the uniform distribution over binary strings of length n + ℓ.

Problem 3: Shamir Secret Splitting

Let (x₁,y₁),…,(x₅,y₅) be shares of a secret s in a (2,5) secret splitting scheme over Z_p. Assume one of the shares has been corrupted and does not lie on the dealer’s polynomial, but nobody knows which the bad share is.

For each value of k = 1,…,5, answer the following questions with respect to an arbitrary subset of shares R of size k.

1. Can it be determined if R contains a bad share? If so, describe how. If not, explain why not.
2. If it can be determined that R contains a bad share, can the bad share be identified? If so, describe how. If not, explain why not.
3. Can the secret s be recovered from R (despite the possible presence of one bad share in R)? If so, describe how. If not, explain why not.
   [Note that you cannot assume that it is necessary to identify the bad share in order to reconstruct the secret; there might well be a procedure that always comes up with the correct s even without knowing which of the shares is bad.]

Problem 4: Oblivious Transfer Variant OT₁^k

The 1-of-k oblivious transfer of a selected secret protocol computes the functionality

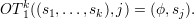
This means that Alice initially has k “secrets” s₁,…,s_k, and Bob initially has the index j of a secret that he would like to know. At the end of the protocol, Bob learns s_j but nothing else, and Alice learns nothing. That is, Alice has no information about Bob’s value j, and Bob has no information about any s_ℓ other than s_j.

Figure 1 gives a protocol for OT₁^k in the semi-honest model.

Questions:

1. Explain why Bob’s output s equals s_j.
2. Explain why Alice learns nothing about j. What assumptions do you have to make about the two cryptosystems involved for this to be true?
3. Explain why Bob learns nothing about s_ℓ for ℓ≠j. What assumptions do you have to make about the two cryptosystems involved for this to be true?
4. If Alice were dishonest, is there anything she could do to learn j? If so, describe how. If not, explain why not.
5. If Bob were dishonest, is there anything he could to do learn secrets other than s_j? If so, describe how. If not, explain why not.

Alice Bob Private input (s1,…,sk). Private input j. 1. Choose k random PKS key pairs (e1,d1),…,(ek,dk). 2. Choose random keys x1,…,xk for symmetric cryptosystem (Ê,). Let yj = Eej(xj), and let yi = xi for all i≠j. 3. Let zi = Ddi(yi), i {1,…,k}. Let ci = Êzi(si), i {1,…,k}. 4. Output s = xj(cj). Figure 1: A protocol to compute OT1k.