| Happy | Bob | ||
| 1. | 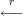 | Choose random string r. | |
| 2. | Compute s = SA(r) | 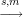 | Check V A(r,s). |
| Accept m as coming from Happy if check succeeds. |
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 467b: Cryptography and Computer Security | Handout #10 | |
| Professor M. J. Fischer | March 28, 2012 | |
Problem Set 5
Due on Wednesday, April 4, 2012.
Instructions Work the problems below, prepare your answers in electronic form, and submit your solutions using the submit script on the Zoo. Remember to specify “5” for the problem number argument to submit.
Problem 1: ElGamal Signature Scheme
Happy Hacker was having trouble understanding the ElGamal signature scheme presented on slide #26, lecture 11. He didn’t see why the signer should bother choosing a random y in step 1 and decided instead to simply fix y = 1. Help Happy out and explain why this is not a good idea.
Problem 2: ElGamal Authentication
Once Happy understood ElGamal signatures, he was excited to use them for authentication. He wants to send an authenticated message m to Bob so that Bob can verify that m came from him.
Here’s his idea. Assume that Happy has an ElGamal signing key (g,p,x) and Bob has the corresponding verification key (g,p,a). We denote the signing algorithm using that key pair by S and the verification algorithm by V .
| Happy | Bob | ||
| 1. | 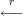 | Choose random string r. | |
| 2. | Compute s = SA(r) | 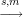 | Check V A(r,s). |
| Accept m as coming from Happy if check succeeds. |
Problem 3: Indistinguishability
Happy’s roommate, Naive Nelson, is building a pseudorandom sequence generator. He has found a PRSG G that takes a 128-bit seed s and outputs a bit string x of length 1000. Naive wants to generate bit strings of length ℓ = 100,000, so he creates a new generator G′ that works in stages. His idea is to use G repeatedly, obtaining 1000 bits each time. To avoid getting repetitions of the same 1000-bit string, he uses the last 128 bits of each block as a seed for the next block.
Here is his algorithm in greater detail for computing G′(s). s0,s1,…,s100 are 128-bit strings, where s0 = s. x1,…,x100 comprise a sequence of 1000-bit strings. xi and si are computed from si-1 as follows: xi = G(si-1). si is the last 128 bits of xi.
Unfortunately, G′(s) is not cryptographically strong. Explain why, and describe a judge J that can distinguish the distribution G′(S) from U. Here, S is the uniform distribution over the seed space, and U is the uniform distribution over binary strings of length ℓ.