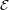Instructions Work the problem below, prepare your answer in electronic form, and submit your solution using the submit script on the Zoo. Remember to specify “7” for the problem number argument to submit.

1 Problem Description

The goal of this assignment is to implement some of the arithmetic needed for elliptic curve cryptography (lecture 13) using the GNU Multiple Precision Arithmetic Library. The GMP integer functions provide most of the tools you will need. Pay special attention to the integer functions portion of GMP. GMP is available on the Zoo machines.

GMP supports both a C and a C++ interface. You may use either one for this assignment. GMP was originally written for C, and much of the documentation refers to the C API’s. If you choose to use C++, you will have to understand how the C++ class interface works.

2 Elliptic Curves over Z_p

For this assignment, we consider the elliptic curve 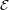over Z_p whose defining equation is

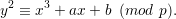(1)

The curve 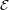consists of all of the points (x,y) Z_p × Z_p that satisfy equation 1, together with a special point “at infinity” denoted 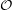. We assume that p is an odd prime and that a and b satisfy the condition

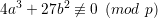(2)

This ensures that the curve is non-singular.

A special kind of addition can be defined on the points in called elliptic curve addition. This operation is usually denoted by the ordinary “+” symbol, but one should remember that its arguments are points, not elements of the field Z_p.

Elliptic curve addition is defined in slides 14 and 15 of lecture 13. Note that there are five defining cases for X + Y depending on whether or not X and Y are the infinity point, and if not, whether or not they agree in their x-coordinates and y-coordinates.

There is also a unary operation of elliptic curve negation, written “-”. As with ordinary arithmetic, negation has the property that -P is the additive inverse of P , so that P + (-P) = (-P) + P = 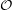. Negation is easily computed. (-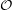) = 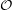, and for a point P = (x,y), (-P) = (x,-y). It follows immediately from case 3 of the definition of addition that P + (-P) = 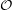as desired. For convenience, one usually defines the binary substraction operator in the usual way as P - Q = P + (-Q).

An elliptic curve is described by three domain parameters p,a,b. We will specify an elliptic curve by a text file that contains a sequence of whitespace-separated unsigned decimal big numbers, the first three of which are p,a,b, respectively. You may assume that p is an odd prime and that a and b satisfy constraint 2.

Elliptic curves support another kind of operation that we call point muliplication. We denote it using the symbol ×, but this is not the usual meaning of multiplication, for the first argument must be a non-negative integer k and the second a point P 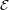. It is defined to be the result of adding P to itself k times. Thus, 3 × P = P + P + P , where P is a point on the elliptic curve. Note that × is “associative” in the sense that the following equation holds for all non-negative integers k and m:

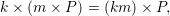
where km is ordinary integer product.

Point multiplication on elliptic curves is analogous to exponentation. aⁿ means to multiply a times itself a total of n times. Similarly, n×P mean to add P to itself a total of n times. In both cases, these are easily computed by a loop that performs n separate operations, and in both cases, this approach becomes infeasible when n is large.

For exponentiation, a fast algorithm based on repeated squaring was presented in lecture 7. A similar technique based in repeated doubling will work to reduce the work to compute n × P from O(n) to O(log n).

Another operation on elliptic curves that is sometimes needed is to find a point on the curve with a given x-value, if it exists. This entails solving equation 1 for y. Of course, if the right hand side is not a quadratic residue modulo p, then no such solution is possible. Recall that Shank’s algorithm from lecture 14 gives a reasonably efficient means of finding modular square roots when they exist. Because the algorithm as presented assumes that the number a whose square root is desired is in QR_p, you should either compute the Legendre symbol to verify that a QR_p before running Shank’s algorithm, or you should modify Shank’s algorithm appropriately so that it detects when a QNR_p and gives an appropriate output.

3 Data representation

External representations Numbers in files are represented as arbitrary precision optionally-signed decimal integers. They can be read and written using mpz_inp_str and mpz_out_str, respectively. (C++ users should be able to use the standard operators >> and <<.)

EC points should be represented by pairs of signed decimal arbitrary precision integers. The special point 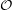is represented by the string “-1 -1”. The point (x,y) is represented by the string “(x)₁₀ (y)₁₀”, where (x)₁₀ and (y)₁₀ are the decimal representations of the non-negative numbers x and y, respectively.

Internal representations Big integers should be represented internally using GMP big integers (type mpz_t if using the C interface, and class mpz_class if using the C++ interface). An EC point should be represented by a struct or class containing two big integers representing the x and y components of the point. Because x and y are always non-negative, the special point 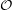can be represented unambiguously by the pair (-1,-1). However, 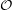must still be tested for and treated specially in your code since it is not correct to compute on this pair as if it were an ordinary EC point.

4 Assignment

You should write functions to do the following:

1. Read a file of EC domain parameters as described above.
2. Read an EC point from an open stream.
3. Write an EC point to an open stream.
4. Add two EC points.
5. Negate an EC point.
6. Subtract two EC points.
7. Perform point multiplication k×P of a big integer k and a point P by the method of repeated doubling.
8. Given a number x Z_p, find y such that the point (x,y) lies on the curve, or return a flag indicating that no such point exists.

In addition to the functions, you should produce one or more programs and data sets to test each of your functions and verify that they work correctly.

For the functions that work on arbitrary size integers, you should test them first with small numbers for which you can verify the answers by hand and make sure they are correct. Then you should test them with numbers that are at least 40 decimal digits long to make sure that the big number arithmetic is working correctly.

Tests of the addition function should include test data that exercises all five cases of the definition. The test for subtraction of P - Q should verify the result R by checking that R + Q = P . Point multiplication should be checked first for small values of k by adding P to itself k times. Then it should be checked for large pairs of number k and m to ensure that k × (m × P) = (km) × P . Finally, to verify the point-on-curve function (8), check that the returned point P satisfies equation 1.

5 Deliverables

You should submit the following items:

1. A makefile, all source code and header files needed to build your project.
2. Test data files and the output from your code when run on them.
3. A brief human-readable document with information about your code such as known bugs, procedures for building and running it, and anything else that might help the grader.

Please be aware that the submit script can only handle files, not whole directory trees.