1: Introduction

The goals of this problem set are:

1. To learn how to use the GNU multiple precision arithmetic library in cryptographic applications.
2. To produce working code for the version of the Elliptic Curve ElGamal cryptosystem presented in lecture 23.

The assignment is broken into several parts. I recommend that you implement the parts in sequence, testing each part before going on to the next. This both will pay off in saved debugging time later on as well as giving a basis for partial credit in case you are unable to complete the assignment. Good coding practice would have you modularize code that is needed in more than one part, but I will leave the question of how to structure your code up to you.

2: GNU Multiple Precision Arithmetic (GMP)

GMP is a highly optimized package for calculating with big numbers. It was originally intended to be used with C. More recently, C++ extensions have been added that make it much easier to use for ordinary calculations, but some of the more sophisticated functions are still only available through the C interface. I have used some of them in implementing the functions in the ECurve class that I will be furnishing to you, but you should not need to call them directly.

Since you will be using the C++ interface, you should pay special attention to section 12 of the GMP manual. You can also read the manual on the Zoo by typing info gmp.

Please feel free to ask for help with C++.

3: File Types

Your programs will be dealing with several different kinds of files.

1. An elliptic curve parameter file contains six whitespace-delimited decimal integers that describe a particular elliptic curve. It has a .ec file extension.

   The numbers, in order, are the values of the elliptic curve parameters p,n,a,b,G_x,G_y. Parameter p is the modulus of the prime field F_p, n is the order of the elliptic subgroup generated by basepoint (G_x,G_y), and a and b are the coefficients in the elliptic curve equation

   

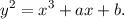
   n is not needed in this assignment, but it is included for completeness.¹

2. The private key for EC ElGamal consists of an elliptic curve, points α and β, and the secret number a. A private key file contains the numbers, in order, that describe each. The elliptic curve is described by 6 numbers, each point by 2 numbers, and the secret is one more for a total of 11 numbers. It has a .prv file extension. For this assignment, we fix α to be the base point (G_x,G_y).²
3. The public key is the same as the private key but without the secret a. It is described by a file of 10 numbers and has a .pub file extension.
4. An EC ElGamal numeric plaintext file consists of b numbers in Z* _p and has file extension .pt.
5. An EC ElGamal ciphertext file consists of a point Y ₁ and an element Y ₂ ∈ Z_p for a total of 3 numbers. A file containing the ciphertext for b plaintext numbers thus contains 3b numbers and has file .ct.
6. A character plaintext file is any text file not containing the null character '\0'. It often has file extension .txt.

4: Assignment Parts

You should write, debug, and test several separate commands.

1. encode curve.ec dat.txt reads the elliptic curve file curve.ec and prints out the parameters, nicely labeled, one per line. Next it checks that the elliptic curve is non-singular and that the basepoint (G_x,G_y) actually lies on the curve. It then calculates and prints out the number of bytes ℓ that can be encoded by an element in Z*_p. This is the largest integer ℓ such that 2^8ℓ < p. Finally, it prints out the file dat.txt in blocks of ℓ characters per line. If the file length is not a multiple of ℓ, then the last line printed will be shorter than ℓ.
2. genkey curve.ec key [seed] generates an EC ElGamal key pair. The public and private keys are written to the files “key.pub” and “key.prv”, respectively.

   The secret a is chosen at random from Z_p using the random number function get_z_range(p) in class gmp_randclass. The constructor for the class must be called with parameter gmp_randinit_default. The generator is seeded from the optional seed parameter, if provided. Otherwise, it is seeded from the number returned by time(0). (See section 12.5 in the GMP manual for how to seed the generator, and look at mpz_class::set_str() in section 12.2 for how to convert the command line string to a big number.)

   The purpose of the optional seed parameter is to facilitate testing of your code. By supplying the seed, the output is reproducible on successive runs of your code.

3. encryptn key.pub data.pt data.ct [seed] reads the private key file key.prv and extracts from it the elliptic curve and the parameters α,β. It then reads each element of data.pt, encrypts it using EC ElGamal, and writes the resulting ciphertext to data.ct. It handles the necessary random number generation and the optional seed command line argument in the same way as genkey.
4. decryptn key.prv data.ct data.pt reads the private key file key.prv and extracts from it the elliptic curve and the parameters α,β,a. It then reads each ciphertext element from data.ct, decrypts it using EC ElGamal, and writes the resulting number to data.ct.

Extra credit: Write functions encrypt and decrypt to work for character plaintext files. Each group of ℓ bytes is converted to a number in Z_p and encrypted as in encryptn. After decryption back to a number in Z_p, the number should be decoded to yield the original text file.

5: Coding Advice

To reduce the amount of tedious code you must write, I am providing you with two C++ class libraries for computing with elliptic curves: ECurve and Point. The corresponding header and object files are in the Zoo directory /c/cs467/assignments/ps7/.

Class ECurve represents an elliptic curve. It has data members for each of the six elliptic curve parameters. One constructor takes the six parameters as arguments. The other reads the parameters from the open input stream argument. In addition, it supports get-functions for accessing the parameters, I/O functions for reading and writing the parameters to files, and five number-theoretic functions for computing with elliptic curves over Z_p:

1. nonSing() returns true if the curve is non-singular and false if not.
2. mod(a) returns the value of a mod p. Note that this implements the mathematical definition of mod that we have been using in class and is not the same as a%p, which implements the C semantics.
3. modexp(a, e) returns the value of a^e mod p.
4. modinv(x) returns the value of x^-1 mod p for x ∈ Z*_p.
5. modsqrt(b, a) returns false if a ∈ QNR_p; otherwise it returns true and sets reference parameter b to a member of 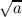mod p.

Class Point represents a coordinate pair (x,y) of numbers. It contains functions for computing in the elliptic curve group as well as utility functions for reading and writing points to files. For those of you who are not C++ experts, the template function Point(T x, T y) : x(x), y(y) is a constructor that works for all integer types, not just big numbers. The point at infinity (which we call the “zero” point) is represented by (-1,-1). It is also the value of the static constant zero.

There are two bool-valued functions:

1. isZero() returns true if ⋆this == zero and false otherwise.
2. onCurve(ec) returns true if the point ⋆this lies on the curve ec and false if not.

Finally, there are four elliptic curve point functions. In all cases, the implicit argument ⋆this is set to the result of the function.

1. add(Q, ec) adds point ⋆this to point Q on the elliptic curve ec.
2. negate ec) negates point ⋆this on the elliptic curve ec.
3. sub(Q, ec) subtracts point Q from point ⋆this on the elliptic curve ec.
4. times(k, P, ec) adds together k copies of point P on the elliptic curve ec.

In both classes, print writes a formatted version of the data, whereas write simply writes out the object as a sequence of whitespace-delimited decimal integers.

To use these classes, you will need to include the furnished header files in your code, and you will need to link against the furnished library file -lps7 and the system libraries -lgmp and -lgmpxx. Assuming your code is in file mycode.cpp and you have copied the contents of the assignment directory to your working directory, then the command

should be enough to compile and link your code.

The Zoo directory also contains sample key and ciphertext files. They were both generated with the seed for the random number generator set to 1234. If your code is correct, you should be able to duplicate these exact files. (Possible variations in the amount and arrangement of whitespace are permissible. Use diff -w to compare your output with mine while ignoring whitespace differences.) See /c/cs467/assignments/ps7/readme for more information about these files.

I know that not all of you are familiar with C and C++ programming. I’ve tried to keep the required programming knowledge to a minimum, but you will obviously have to know some of the basics such as how to read and write from files, how to read and process the command line, and how to make simple use of a class. Please start early on this assignment and feel free to ask for help.