YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 467b: Cryptography and Computer Security | Handout #6 |
| Professor M. J. Fischer | | February 18, 2013 |
|
|
|
| |
Linear Congruence Equations
Let a,x  Z*
n. Recall that x is said to be an inverse of a modulo n if ax ≡ 1 (mod n). It is easily seen
that the inverse, if it exists, is unique modulo n, for if ax ≡ 1 (mod n) and ay ≡ 1 (mod n), then
x ≡ xay ≡ y (mod n). We denote this unique x, when it exists, by a-1 (mod n) (or simply a-1 when
the modulus n is clear from context).
Z*
n. Recall that x is said to be an inverse of a modulo n if ax ≡ 1 (mod n). It is easily seen
that the inverse, if it exists, is unique modulo n, for if ax ≡ 1 (mod n) and ay ≡ 1 (mod n), then
x ≡ xay ≡ y (mod n). We denote this unique x, when it exists, by a-1 (mod n) (or simply a-1 when
the modulus n is clear from context).
Theorem 1 Let a  Z*n. Then a-1 exists in Z*n.
Z*n. Then a-1 exists in Z*n.
Proof: Let a  Z*n and consider the function fa(x) = ax mod n. fa is easily shown to be a
one-one mapping from Z*n to Z*n. Hence, fa is also onto, so for some x
Z*n and consider the function fa(x) = ax mod n. fa is easily shown to be a
one-one mapping from Z*n to Z*n. Hence, fa is also onto, so for some x  Z*n, fa(x) = 1. Then
ax ≡ 1 (mod n), so x = a-1 (mod n). __
Z*n, fa(x) = 1. Then
ax ≡ 1 (mod n), so x = a-1 (mod n). __
We showed in class how to use the Extended Euclidian algorithm to efficiently compute a-1 (mod n) given a
and n.
Here we consider the solvability of the more general linear congruence equation:
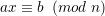 | (1) |
where a,b  Z*n are constants, and x is a variable ranging over Z*n.
Z*n are constants, and x is a variable ranging over Z*n.
Proof: Let d = gcd(a,n). Clearly if ax ≡ b (mod n), then d∣b, so there are no solutions if d ~ ∣ b.
Now suppose d∣b. Since (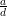 ) and (
) and (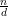 ) are relatively prime,
) are relatively prime,  exists by Theorem 1. Multiplying both
sides of (2) by a, we get
exists by Theorem 1. Multiplying both
sides of (2) by a, we get
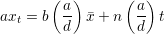 | (3) |
where now we are working over the integers. But 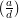
 = 1 +
= 1 + 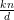 for some k by the definition of
for some k by the definition of  , so
substituting for
, so
substituting for 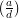
 in (3) yields
in (3) yields
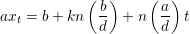 | (4) |
The quantities in parentheses are both integers, so it follows immediately that axt ≡ b (mod n) and hence
xt is a solution of (1).
It remains to show that the d solutions above are distinct modulo n. But this is obvious since
x0 < x1 < … < xd-1 and xd-1 - x0 = 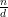 (d - 1) < n. __
(d - 1) < n. __
 Z*
n. Recall that x is said to be an inverse of a modulo n if ax ≡ 1 (mod n). It is easily seen
that the inverse, if it exists, is unique modulo n, for if ax ≡ 1 (mod n) and ay ≡ 1 (mod n), then
x ≡ xay ≡ y (mod n). We denote this unique x, when it exists, by a-1 (mod n) (or simply a-1 when
the modulus n is clear from context).
Z*
n. Recall that x is said to be an inverse of a modulo n if ax ≡ 1 (mod n). It is easily seen
that the inverse, if it exists, is unique modulo n, for if ax ≡ 1 (mod n) and ay ≡ 1 (mod n), then
x ≡ xay ≡ y (mod n). We denote this unique x, when it exists, by a-1 (mod n) (or simply a-1 when
the modulus n is clear from context).
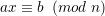
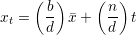

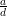
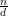
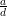
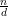
 exists by Theorem
exists by Theorem 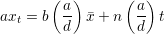
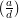

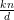 for some
for some  , so
substituting for
, so
substituting for 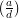
 in (
in (