YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE

	CPSC 467: Cryptography and Computer Security	Handout #8
Professor M. J. Fischer		October 23, 2017

Homework Assignment 6

Due on Monday, October 30, 2017.

Problem 1: Elliptic curve parameters

Consider the elliptic curve with parameters a, b, and p defined by

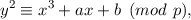
2 3 y ≡ x + ax + b (mod p),

For each parameter triple (a,b,p), say whether or not the resulting elliptic curve satisfies the definition for an elliptic curve modulo a prime given on slide 10 of lecture 13, and explain your answers.

a b p ----------------- i. 1 0 3 ii. 3 - 2 7 iii. 0 0 13 iv. 0 3 15 v. 0 3 17

Problem 2: Elliptic curve group

List all points in the elliptic curve group defined by

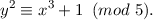
y2 ≡ x3 + 1 (mod 5).

Problem 3: Elliptic curve addition

The points P = (0,3) and Q = (4,2) are in the elliptic curve group defined by

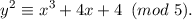
y2 ≡ x3 + 4x + 4 (mod 5).

(See slide 14 of lecture 13.) What is P + Q? Show your work.

Problem 4: Zero divisors

An element a ∈ Z_n -{0} is said to be a zero divisor modulo n if ab ≡ 0 (mod n) for some b ∈ Z_n -{0}.

Explain why there are no zero divisors in Z_p when p is prime.
Find a zero divisor in Z₂₁.
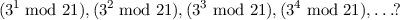
What is the value of the first element to repeat in the sequence $(31 mod 21),(32 mod 21),(33 mod 21),(34 mod 21),...?$

In all cases, justify your answers.

Problem 5: Greatest common divisor

The definition of greatest common divisor can be extended naturally to a sequence of numbers (a₁,a₂,…,a_k), not all of which are zero; namely, it is the largest integer d ≥ 1 such that d∣a_j for all j = 1,2,…,k. Describe an efficient algorithm for computing gcd(a₁,…,a_k), and explain why it computes the correct answer.

Problem 6: Euler’s totient function

Compute ϕ(3500). Show your work.

Problem 7: Euler theorem

Compute 3⁹⁰⁷²¹¹ mod 3500.

Problem 8: Extended Euclidean algorithm

Use the extended Euclidean algorithm to solve the Diaphantine equation 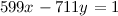$599x - 711y = 1$ . Show the resulting table of triples as in slide 15 of lecture 14 notes.
[Note: You may write a program to produce the table if you wish, but these numbers are small enough to make it quite feasible to carry out the computation by hand or with the aid of a pocket calculator.]