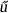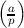YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE

	CPSC 467: Cryptography and Computer Security	Handout #11
Professor M. J. Fischer		November 13, 2017

Number Theory Summary

Integers: Let Z denote the integers and Z+ the positive integers.
Division: For a ∈ Z and n ∈ Z+, there exist unique integers q,r such that a = nq + r and 0 ≤ r < n. We denote the quotient q by ⌊a∕n⌋ and the remainder r by a mod n. We say n divides a (written n∣a) if a mod n = 0. If n∣a, n is called a divisor of a. If also 1 < n < |a|, n is said to be a proper divisor of a.
Greatest common divisor: The greatest common divisor (gcd) of integers a,b (written gcd(a,b) or simply (a,b)) is the greatest integer d such that d∣a and d∣b. If gcd(a,b) = 1, then a and b are said to be relatively prime.
Euclidean algorithm: Computes gcd(a,b). Based on two facts: gcd(0,b) = b; gcd(a,b) = gcd(b,a - qb) for any q ∈ Z. For rapid convergence, take q = ⌊a∕b⌋, in which case a - qb = a mod b.
Congruence: For a,b ∈ Z and n ∈ Z+, we write a ≡ b (mod n) iff n∣(b-a). Note a ≡ b (mod n) iff (a mod n) = (b mod n).
Modular arithmetic: Fix n ∈ Z+. Let Z_n = {0,1,…,n - 1} and let Z*_n = {a ∈ Z_n∣gcd(a,n) = 1}. For integers a,b, define a ⊕ b = (a + b) mod n and a ⊗ b = ab mod n. ⊕ and ⊗ are associative and commutative, and ⊗ distributes over ⊕. Moreover, mod n distributes over both + and ×, so for example, a + b × (c + d) mod n = (a mod n) + (b mod n) × ((c mod n) + (d mod n)) = a⊕b⊗ (c⊕d). Z_n is closed under ⊕ and ⊗, and Z*_n is closed under ⊗.
Primes and prime factorization: A number p ≥ 2 is prime if it has no proper divisors. Any positive number n can be written uniquely (up to the order of the factors) as a product of primes. Equivalently, there exist unique integers k,p₁,…,p_k,e₁,…,e_k such that n = ∏ _i=1^kp_i^e_i, k ≥ 0, p₁ < p₂ < … < p_k are primes, and each e_i ≥ 1. The product ∏ _i=1^kp_i^e_i is called the prime factorization of n. A positive number n is composite if (∑ _i=1^ke_i) ≥ 2 in its prime factorization. By these definitions, n = 1 has prime factorization with k = 0, so 1 is neither prime nor composite.
Linear congruences: Let a,b ∈ Z, n ∈ Z+. Let d = gcd(a,n). If d∣b, then there are d solutions x in Z_n to the congruence equation ax ≡ b (mod n). If d ~ ∣ b, then ax ≡ b (mod n) has no solution.
Extended Euclidean algorithm: Finds one solution of ax ≡ b (mod n), or announces that there are none. Call a triple (g,u,v) valid if g = au + nv. Algorithm generates valid triples starting with (n,0,1) and (a,1,0). Goal is to find valid triple (g,u,v) such that g∣b. If found, then u(b∕g) solves ax ≡ b (mod n). If none exists, then no solution. Given valid (g,u,v), (g′,u′,v′), can generate new valid triple (g - qg′,u - qu′,v - qv′) for any q ∈ Z. For rapid convergence, choose q = ⌊g∕g′⌋, and retain always last two triples. Note: Sequence of generated g-values is exactly the same as the sequence of numbers generated by the Euclidean algorithm.
Inverses: Let n ∈ Z+, a ∈ Z. There exists unique b ∈ Z such that ab ≡ 1 (mod n) iff gcd(a,n) = 1. Such a b, when it exists, is called an inverse of a modulo n. We write a^-1 for the unique inverse of a modulo n that is also in Z_n. Can find a^-1 mod n efficiently by using Extended Euclidean algorithm to solve ax ≡ 1 (mod n).
Euler function: Let ϕ(n) = |Z*_n|. One can show that ϕ(n) = ∏ _i=1^k(p_i - 1)p_i^e_i-1, where ∏ _i=1^kp_i^e_i is the prime factorization of n. In particular, if p is prime, then ϕ(p) = p - 1, and if p,q are distinct primes, then ϕ(pq) = (p - 1)(q - 1).
Euler’s theorem: Let n ∈ Z+, a ∈ Z*_n. Then a^ϕ(n) ≡ 1 (mod n). As a consequence, if r ≡ s (mod ϕ(n)) then a^r ≡ a^s (mod n).
Order of an element: Let n ∈ Z+, a ∈ Z*_n. We define ord(a), the order of a modulo n, to be the smallest number k ≥ 1 such that a^k ≡ 1 (mod n). Fact: ord(a)∣ϕ(n).
Primitive roots: Let n ∈ Z+, a ∈ Z*_n. a is a primitive root of n iff ord(a) = ϕ(n). For a primitive root a, it follows that Z*_n = {a mod n,a² mod n,…,a^ϕ(n) mod n}. If n has a primitive root, then it has ϕ(ϕ(n)) primitive roots. Primitive roots exist for every prime p (and for some other numbers as well). a is a primitive root of p iff a^(p-1)∕q ⁄≡ 1 (mod p) for every prime divisor q of p - 1.
Discrete log: Let p be a prime, a a primitive root of p, b ∈ Z*_p such that b ≡ a^k (mod p) for some k, 0 ≤ k ≤ p - 2. We say k is the discrete logarithm of b to the base a.
Chinese remainder theorem: Let n₁,…,n_k be pairwise relatively prime numbers in Z+, let a₁,…,a_k be integers, and let n = ∏ _in_i. There exists a unique x ∈ Z_n such that x ≡ a_i (mod n_i) for all 1 ≤ i ≤ k. To compute x, let N_i = n∕n_i and compute M_i = N_i^-1 mod n_i, 1 <= i <= k. Then x = (∑ _i=1^ka_iM_iN_i) mod n.
Quadratic residues: Let a ∈ Z, n ∈ Z+. a is a quadratic residue modulo n if there exists y such that a ≡ y² (mod n). a is sometimes called a square and y its square root.
Quadratic residues modulo a prime: If p is an odd prime, then every quadratic residue in Z*_p has exactly two square roots in Z*_p, and exactly half of the elements in Z*_p are quadratic residues. Let a ∈ Z*_p be a quadratic residue. Then a^(p-1)∕2 ≡ (y²)^(p-1)∕2 ≡ y^p-1 ≡ 1 (mod p), where y a square root of a modulo p. Let g be a primitive root modulo p. If a ≡ g^k (mod p), then a is a quadratic residue modulo p iff k is even, in which case its two square roots are g^k∕2 mod p and -g^k∕2 mod p. If p ≡ 3 (mod 4) and a ∈ Z*_p is a quadratic residue modulo p, then a^(p+1)∕4 is a square root of a, since (a^(p+1)∕4)² ≡ aa^(p-1)∕2 ≡ a (mod p).
Quadratic residues modulo products of two primes: If n = pq for p,q distinct odd primes, then every quadratic residue in Z*_n has exactly four square roots in Z*_n, and exactly 1/4 of the elements in Z*_n are quadratic residues. An element a ∈ Z*_n is a quadratic residue modulo n iff it is a quadratic residue modulo p and modulo q. The four square roots of a can be found from its two square roots modulo p and its two square roots modulo q using the Chinese remainder theorem.
Legendre symbol: Let a ≥ 0, p an odd prime. = 1 if a is a quadratic residue modulo p, -1 if a is a quadratic non-residue modulo p, and 0 if p∣a. Fact: 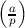= a^(p-1)∕2.
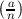Jacobi symbol: Let a ≥ 0, n an odd positive number with prime factorization ∏ _i=1^kp_i^e_i. We define = ∏ _i=1^k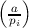^e_i. (By convention, this product is 1 when k = 0, so 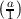= 1.) The Jacobi and Legendre symbols agree when n is an odd prime. If 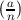= -1 then a is definitely not a quadratic residue modulo n, but if 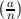= 1, a might or might not be a quadratic residue.
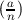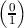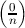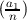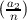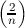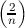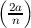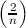
Computing the Jacobi symbol: can be computed efficiently by a straightforward recursive algorithm, based on the following identities: = 1; = 0 for n≠1; = if a₁ ≡ a₂ (mod n); = 1 if n ≡ ±1 (mod 8); = -1 if n ≡ ±3 (mod 8); = 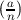; 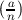= 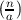if a ≡ 1 (mod 4) or n ≡ 1 (mod 4); 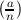= - 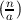if a ≡ n ≡ 3 (mod 4).
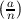Solovay-Strassen test for compositeness: Let n ∈ Z+. If n is composite, then for roughly 1/2 of the numbers a ∈ Z*_n, ⁄≡ a^(n-1)∕2 (mod n). If n is prime, then for every a ∈ Z*_n, 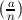≡ a^(n-1)∕2 (mod n).
Miller-Rabin test for compositeness: Let n ∈ Z+ and write n-1 = 2^km, where m is odd. Choose 1 ≤ a ≤ n - 1. Compute b_i = a^m2ⁱ mod n for i = 0,1,…,k - 1. If n is composite, then for roughly 3∕4 of the possible values for a, b₀≠1 and b_i≠ - 1 for 0 ≤ i ≤ k - 1. If n is prime, then for every a, either b₀ = 1 or b_i = -1 for some i, 0 ≤ i ≤ k - 1.

Michael J. Fischer
(Thanks to Miklós Csrös, Andrei Serjantov, and Jerry Moon for pointing out errors in previous drafts.)
Last modified: February 16, 2012.