Reinforcement Learning¶
This Jupyter notebook acts as supporting material for Chapter 21 Reinforcement Learning of the book Artificial Intelligence: A Modern Approach. This notebook makes use of the implementations in rl.py module. We also make use of implementation of MDPs in the mdp.py module to test our agents. It might be helpful if you have already gone through the Jupyter notebook dealing with Markov decision process. Let us import everything from the rl module. It might be helpful to view the source of some of our implementations. Please refer to the Introductory Jupyter notebook for more details.
from rl import *
CONTENTS¶
- Overview
- Passive Reinforcement Learning
- Direct Utility Estimation
- Adaptive Dynamic Programming
- Temporal-Difference Agent
- Active Reinforcement Learning
- Q learning
OVERVIEW¶
Before we start playing with the actual implementations let us review a couple of things about RL.
Reinforcement Learning is concerned with how software agents ought to take actions in an environment so as to maximize some notion of cumulative reward.
Reinforcement learning differs from standard supervised learning in that correct input/output pairs are never presented, nor sub-optimal actions explicitly corrected. Further, there is a focus on on-line performance, which involves finding a balance between exploration (of uncharted territory) and exploitation (of current knowledge).
-- Source: Wikipedia
In summary we have a sequence of state action transitions with rewards associated with some states. Our goal is to find the optimal policy $\pi$ which tells us what action to take in each state.
PASSIVE REINFORCEMENT LEARNING¶
In passive Reinforcement Learning the agent follows a fixed policy $\pi$. Passive learning attempts to evaluate the given policy $pi$ - without any knowledge of the Reward function $R(s)$ and the Transition model $P(s'\ |\ s, a)$.
This is usually done by some method of utility estimation. The agent attempts to directly learn the utility of each state that would result from following the policy. Note that at each step, it has to perceive the reward and the state - it has no global knowledge of these. Thus, if a certain the entire set of actions offers a very low probability of attaining some state $s_+$ - the agent may never perceive the reward $R(s_+)$.
Consider a situation where an agent is given a policy to follow. Thus, at any point it knows only its current state and current reward, and the action it must take next. This action may lead it to more than one state, with different probabilities.
For a series of actions given by $\pi$, the estimated utility $U$: $$U^{\pi}(s) = E(\sum_{t=0}^\inf \gamma^t R^t(s')$$) Or the expected value of summed discounted rewards until termination.
Based on this concept, we discuss three methods of estimating utility:
Direct Utility Estimation (DUE)
The first, most naive method of estimating utility comes from the simplest interpretation of the above definition. We construct an agent that follows the policy until it reaches the terminal state. At each step, it logs its current state, reward. Once it reaches the terminal state, it can estimate the utility for each state for that iteration, by simply summing the discounted rewards from that state to the terminal one.
It can now run this 'simulation' $n$ times, and calculate the average utility of each state. If a state occurs more than once in a simulation, both its utility values are counted separately.
Note that this method may be prohibitively slow for very large statespaces. Besides, it pays no attention to the transition probability $P(s'\ |\ s, a)$. It misses out on information that it is capable of collecting (say, by recording the number of times an action from one state led to another state). The next method addresses this issue.
Adaptive Dynamic Programming (ADP)
This method makes use of knowledge of the past state $s$, the action $a$, and the new perceived state $s'$ to estimate the transition probability $P(s'\ |\ s,a)$. It does this by the simple counting of new states resulting from previous states and actions.
The program runs through the policy a number of times, keeping track of:- each occurrence of state $s$ and the policy-recommended action $a$ in $N_{sa}$
- each occurrence of $s'$ resulting from $a$ on $s$ in $N_{s'|sa}$.
It can thus estimate $P(s'\ |\ s,a)$ as $N_{s'|sa}/N_{sa}$, which in the limit of infinite trials, will converge to the true value.
Using the transition probabilities thus estimated, it can applyPOLICY-EVALUATIONto estimate the utilities $U(s)$ using properties of convergence of the Bellman functions.Temporal-difference learning (TD)
Instead of explicitly building the transition model $P$, the temporal-difference model makes use of the expected closeness between the utilities of two consecutive states $s$ and $s'$. For the transition $s$ to $s'$, the update is written as: $$U^{\pi}(s) \leftarrow U^{\pi}(s) + \alpha \left( R(s) + \gamma U^{\pi}(s') - U^{\pi}(s) \right)$$ This model implicitly incorporates the transition probabilities by being weighed for each state by the number of times it is achieved from the current state. Thus, over a number of iterations, it converges similarly to the Bellman equations. The advantage of the TD learning model is its relatively simple computation at each step, rather than having to keep track of various counts. For $n_s$ states and $n_a$ actions the ADP model would have $n_s \times n_a$ numbers $N_{sa}$ and $n_s^2 \times n_a$ numbers $N_{s'|sa}$ to keep track of. The TD model must only keep track of a utility $U(s)$ for each state.
Demonstrating Passive agents¶
Passive agents are implemented in rl.py as various Agent-Classes.
To demonstrate these agents, we make use of the GridMDP object from the MDP module. sequential_decision_environment is similar to that used for the MDP notebook but has discounting with $\gamma = 0.9$.
The Agent-Program can be obtained by creating an instance of the relevant Agent-Class. The __call__ method allows the Agent-Class to be called as a function. The class needs to be instantiated with a policy ($\pi$) and an MDP whose utility of states will be estimated.
from mdp import sequential_decision_environment
The sequential_decision_environment is a GridMDP object as shown below. The rewards are +1 and -1 in the terminal states, and -0.04 in the rest. 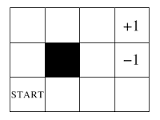 Now we define actions and a policy similar to Fig 21.1 in the book.
Now we define actions and a policy similar to Fig 21.1 in the book.
# Action Directions
north = (0, 1)
south = (0,-1)
west = (-1, 0)
east = (1, 0)
policy = {
(0, 2): east, (1, 2): east, (2, 2): east, (3, 2): None,
(0, 1): north, (2, 1): north, (3, 1): None,
(0, 0): north, (1, 0): west, (2, 0): west, (3, 0): west,
}
Direction Utility Estimation Agent¶
The PassiveDEUAgent class in the rl module implements the Agent Program described in Fig 21.2 of the AIMA Book. PassiveDEUAgent sums over rewards to find the estimated utility for each state. It thus requires the running of a number of iterations.
%psource PassiveDUEAgent
DUEagent = PassiveDUEAgent(policy, sequential_decision_environment)
for i in range(200):
run_single_trial(DUEagent, sequential_decision_environment)
DUEagent.estimate_U()
The calculated utilities are:
print('\n'.join([str(k)+':'+str(v) for k, v in DUEagent.U.items()]))
Adaptive Dynamic Programming Agent¶
The PassiveADPAgent class in the rl module implements the Agent Program described in Fig 21.2 of the AIMA Book. PassiveADPAgent uses state transition and occurrence counts to estimate $P$, and then $U$. Go through the source below to understand the agent.
%psource PassiveADPAgent
We instantiate a PassiveADPAgent below with the GridMDP shown and train it over 200 iterations. The rl module has a simple implementation to simulate iterations. The function is called run_single_trial.
ADPagent = PassiveADPAgent(policy, sequential_decision_environment)
for i in range(200):
run_single_trial(ADPagent, sequential_decision_environment)
The calculated utilities are:
print('\n'.join([str(k)+':'+str(v) for k, v in ADPagent.U.items()]))
Passive Temporal Difference Agent¶
PassiveTDAgent uses temporal differences to learn utility estimates. We learn the difference between the states and backup the values to previous states. Let us look into the source before we see some usage examples.
%psource PassiveTDAgent
In creating the TDAgent, we use the same learning rate $\alpha$ as given in the footnote of the book on page 837.
TDagent = PassiveTDAgent(policy, sequential_decision_environment, alpha = lambda n: 60./(59+n))
Now we run 200 trials for the agent to estimate Utilities.
for i in range(200):
run_single_trial(TDagent,sequential_decision_environment)
The calculated utilities are:
print('\n'.join([str(k)+':'+str(v) for k, v in TDagent.U.items()]))
Comparison with value iteration method¶
We can also compare the utility estimates learned by our agent to those obtained via value iteration.
Note that value iteration has a priori knowledge of the transition table $P$, the rewards $R$, and all the states $s$.
from mdp import value_iteration
The values calculated by value iteration:
U_values = value_iteration(sequential_decision_environment)
print('\n'.join([str(k)+':'+str(v) for k, v in U_values.items()]))
Evolution of utility estimates over iterations¶
We can explore how these estimates vary with time by using plots similar to Fig 21.5a. We will first enable matplotlib using the inline backend. We also define a function to collect the values of utilities at each iteration.
%matplotlib inline
import matplotlib.pyplot as plt
def graph_utility_estimates(agent_program, mdp, no_of_iterations, states_to_graph):
graphs = {state:[] for state in states_to_graph}
for iteration in range(1,no_of_iterations+1):
run_single_trial(agent_program, mdp)
for state in states_to_graph:
graphs[state].append((iteration, agent_program.U[state]))
for state, value in graphs.items():
state_x, state_y = zip(*value)
plt.plot(state_x, state_y, label=str(state))
plt.ylim([0,1.2])
plt.legend(loc='lower right')
plt.xlabel('Iterations')
plt.ylabel('U')
Here is a plot of state $(2,2)$.
agent = PassiveTDAgent(policy, sequential_decision_environment, alpha=lambda n: 60./(59+n))
graph_utility_estimates(agent, sequential_decision_environment, 500, [(2,2)])
It is also possible to plot multiple states on the same plot. As expected, the utility of the finite state $(3,2)$ stays constant and is equal to $R((3,2)) = 1$.
graph_utility_estimates(agent, sequential_decision_environment, 500, [(2,2), (3,2)])
ACTIVE REINFORCEMENT LEARNING¶
Unlike Passive Reinforcement Learning in Active Reinforcement Learning we are not bound by a policy pi and we need to select our actions. In other words the agent needs to learn an optimal policy. The fundamental tradeoff the agent needs to face is that of exploration vs. exploitation.
QLearning Agent¶
The QLearningAgent class in the rl module implements the Agent Program described in Fig 21.8 of the AIMA Book. In Q-Learning the agent learns an action-value function Q which gives the utility of taking a given action in a particular state. Q-Learning does not required a transition model and hence is a model free method. Let us look into the source before we see some usage examples.
%psource QLearningAgent
The Agent Program can be obtained by creating the instance of the class by passing the appropriate parameters. Because of the call method the object that is created behaves like a callable and returns an appropriate action as most Agent Programs do. To instantiate the object we need a mdp similar to the PassiveTDAgent.
Let us use the same GridMDP object we used above. Figure 17.1 (sequential_decision_environment) is similar to Figure 21.1 but has some discounting as gamma = 0.9. The class also implements an exploration function f which returns fixed Rplus until agent has visited state, action Ne number of times. This is the same as the one defined on page 842 of the book. The method actions_in_state returns actions possible in given state. It is useful when applying max and argmax operations.
Let us create our object now. We also use the same alpha as given in the footnote of the book on page 837. We use Rplus = 2 and Ne = 5 as defined on page 843. Fig 21.7
q_agent = QLearningAgent(sequential_decision_environment, Ne=5, Rplus=2,
alpha=lambda n: 60./(59+n))
Now to try out the q_agent we make use of the run_single_trial function in rl.py (which was also used above). Let us use 200 iterations.
for i in range(200):
run_single_trial(q_agent,sequential_decision_environment)
Now let us see the Q Values. The keys are state-action pairs. Where different actions correspond according to:
north = (0, 1) south = (0,-1) west = (-1, 0) east = (1, 0)
q_agent.Q
The Utility U of each state is related to Q by the following equation.
U (s) = max a Q(s, a)
Let us convert the Q Values above into U estimates.
U = defaultdict(lambda: -1000.) # Very Large Negative Value for Comparison see below.
for state_action, value in q_agent.Q.items():
state, action = state_action
if U[state] < value:
U[state] = value
U
Let us finally compare these estimates to value_iteration results.
print(value_iteration(sequential_decision_environment))