Problem : Compute the outcome classes for 0 through 16 for 1-row misere Nim where the legal moves are to take 1, 4, or 5 stones.

Problem : Consider a normal game played with $n$ rows of stones. On each turn, the current player can take any number of stones from any row, or may move any number of stones to the row directly above it (including to a row that has been emptied, not skipping over any row that has not been emptied, and not to a row that never existed).

• Explain why the state with 3 rows of one stone each cannot be viewed simply as the sum of three subgames.
• Compute the Grundy numbers for all positions in this game reachable from an initial position with 3 rows of 1 stone each.
• Compute a winning move in the summed game consisting of two independent copies of the original game (stones cannot move between copies), for the position with the 1st game in the inital position of one with 3 rows with one stone each, and the other game with just one stone left in the middle position (1/1/1 + 0/1/0), or determine that no winning move exists. Repeat for (1/1/1 + 0/2/0).
• How many positions with 5 total stones are reachable from 0/0/6?

Problem : Prove or disprove: for any position $G \approx *n$ and any $m \lt n$, there is an option $G'$ of $G$ such that $G + G' \approx *m$.

Problem :

• Coino is a game played with $n$ coins. On each turn, the player chooses how many of the remaining coins to flip. The player earns one point for each head. If the flip results in at least as many tails as heads then loses the flipped coins for the rest of the game. The game is over when the player is out of coins or reaches $k$ points. The player wins after reaching $k$ points and loses after running out of coins with $\lt k$ points. Write a program that computes the strategy for Coino that maximizes the probability of winning and determines that maximum probability.
• Suppose we modify Coino so that you get one do-over: at most once during the game you may discard the result of a flip and reflip any number of coins if the initial result was not to your liking. How would you modify the algorithm to find the optimal strategy and the expected winning percentage in this case?

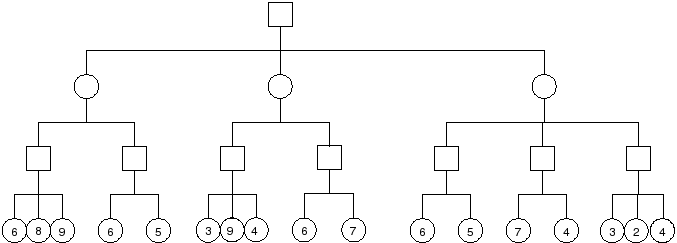
Problem : Compute the minimax value of each node in the tree below. Squares represent max nodes and circles represent min nodes.

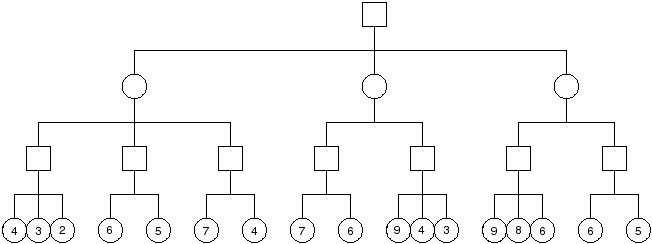
Problem : Show the operation of alpha-beta pruning on the tree shown below. Show the (alpha, beta) windows passed to each node as the tree is traversed, the values returned from each node, and which branches are pruned.

Problem : Consider a constant-sum game with payoff matrix $$\left( \begin{array}{ccc} 0 & 2 & -1 \\ 1 & -2 & 0 \\ -2 & 0 & 2 \end{array} \right)$$.

• Find $v^-$ and $v^+$ for this game.
• Does this game have an equilibrium in pure strategies?
• Compute the value of $E(X,Y)$ for $X=(0 {1 \over 2} {1 \over 2})$ and $Y=({2 \over 3} 0 {1 \over 3})$.
• Using Theorem 1.3.8c, verify that $X^*=({2 \over 5} {2 \over 5} {1 \over 5})$,$Y^*=({2 \over 5} {1 \over 5} {2 \over 5})$ is a saddle point for this game.
• Find player I's best response to $Y=({1 \over 3} {1 \over 3} {1 \over 3})$.

Problem : Find a saddle point and its value for the constant-sum game with payoff matrix $$ \left( \begin{array}{cc} 3 & 2 \\ 0 & 4 \\ \end{array} \right) $$

Problem : Set up the linear program to find a saddle point for the constant-sum game with payoff matrix $$ \left( \begin{array}{ccc} 4 & 7 & 3 \\ 0 & 5 & 4 \\ 10 & 6 & 2 \\ \end{array} \right) $$