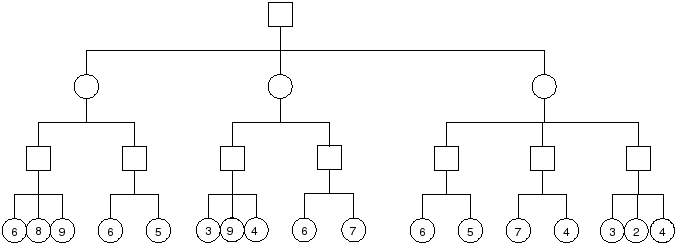
Problem : Compute the minimax value of each node in the tree below. Squares represent max nodes and circles represent min nodes.
Problem : Show the operation of alpha-beta pruning on the tree shown below. Show the (alpha, beta) windows passed to each node as the tree is traversed, the values returned from each node, and which branches are pruned.
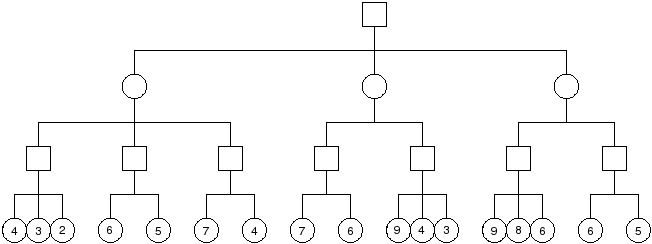
| Node | $(\alpha, \beta)$ | Value |
|---|---|---|
| A | $(-\infty, \infty)$ | 7 |
| B | $(-\infty, \infty)$ | 4 |
| C | $(4, \infty)$ | 7 |
| D | $(7, \infty)$ | 6 |
| E | $(-\infty, \infty)$ | 4 |
| F | $(-\infty, 4)$ [prunes 2nd child] | 6 |
| G | $(-\infty, 4)$ [prunes 2nd child] | 7 |
| H | $(4, \infty)$ | 7 |
| I | $(4, 7)$ [prunes 2nd, 3rd children] | 9 |
| J | $(7, \infty)$ | 9 |
| K | $(7, 9)$ | 6 |
Problem : Show the operation of Scout on he tree from the previous problem. Show the (alpha, beta) windows passed to each node as the tree is traversed, the values returned from each node, and which branches are pruned.
| Node | $(\alpha, \beta)$ | Value |
|---|---|---|
| A | $(-\infty, \infty)$ | 7 |
| B | $(-\infty, \infty)$ | 4 |
| C | $(4, 5)$ $(7, \infty)$ [prunes second child] |
7 7 |
| D | $(7, 8)$ | 6 |
| E | $(-\infty, \infty)$ | 4 |
| F | $(3, 4)$ [prunes 2nd child] | 6 |
| G | $(3, 4)$ [prunes 2nd child] | 7 |
| H | $(4, 5)$ [prunes 2nd child] $(7, \infty)$ |
7 7 |
| I | $(4, 5)$ [prunes 2nd, 3rd children] | 9 9 |
| J | $(7, 8)$ [prunes 2nd, 3rd children] | 9 |
| K | $(7, 8)$ | 6 |
Problem : Show what would be stored in the transposition table after using alpha-beta pruning on the tree from above. Assume that the transposition table is initially empty and there are no collisions.
| Node | Depth | Bound |
|---|---|---|
| A | 3 | =7 |
| B | 2 | =4 |
| C | 2 | =7 |
| D | 2 | =6 |
| E | 1 | =4 |
| F | 1 | ≥6 |
| G | 1 | ≥7 |
| H | 1 | =7 |
| I | 1 | ≥9 |
| J | 1 | =9 |
| K | 1 | =6 |
Problem : Condsider the multi-armed bandit problem with 3 arms with payoffs determined by the outcomes of rolling a fair 6-, 8-, or 10-sided die. Show that the greedy strategy does not achieve zero average regret for this setup.
Problem : Describe modifcations that would be necessary to standard MCTS for 2-player Yahtzee.
Problem : Pick an two enhancements to standard MCTS and describe how they might be applied to NFL Strategy, Kalah, or Yahtzee.
Predicate Average Sampling Technique: for NFL Strategy, use predicates "trailing by more than 21 points" and "leading by more than 21 points" and keep track of the success of various plays in those situations during random playouts. Then bias play selection towards the plays that are better in those situations when in positions matching those situations.
Search Seeding: use a heuristic function for Kalah (perhaps our simple score margin heuristic) to initialize visit count and reward statistics for newly expanded nodes in the hopes of reducing the amount of time determining that bad moves are in fact bad.
Problem : Describe how you would set up the inputs to a neural network that chooses plays for NFL Strategy. Describe how you would use the outputs to choose a play.
- distance to goal line, normalized to $[0.0, 1.0)$
- time left in quarter, normalized to $[0.0, 1.0)$
- current quarter (1.0 = 1st, 0.66 = 2nd, 0.33 = 3rd, 0.0 = 4th)
- current down (1.0 = 1st, 0.66 = 2nd, 0.33 = 3rd, 0.0 = 4th)
- yards to first down divided by 10 (this one is interesting: we should normalize somehow, but dividing by 100 would result in compressing the most frequently seen positions to a small range; normalizing to standard deviations away from the mean seen during actual play may be better)
- score margin divided by 20 (again, the best normalization may be determined by experimentation)
- (and field position as -1 for left, 0, for center, 1 for right if you wish to include that feature of the commercial game)
- one output for each play, interpreted as the probability of selecting that play (so the output layer should use a softmax activation function)
Problem : How did DeepMind address the issue of overfitting when training the value network they used in AlphaGo?