-

> > > > Homework > Exam #1 Practice > Solutions

Problem : Compute the position values for 0 through 16 for 1-row misere Nim where the legal moves are to take 1, 4, or 5 stones.

n012345678910111213141516
outcome classNPNPNNNNNPNPNNNNN

Problem : Consider a normal game played with $n$ rows of stones. On each turn, the current player can take any number of stones from any row, or may move any number of stones to the row directly above it (including to a row that has been emptied, not skipping over any row that has not been emptied, and not to a row that never existed).

Problem : Prove or disprove: for any position $G \approx *n$ and any $m < n$, there is an option $G'$ of $G$ such that $G + G' \approx *m$.

Counterexample: Let $G = *2$ amd $m = 1$. The only options from $G$ are $*1$ and $*0$, but $*2 + *1 \approx *3$ and $*2 + *0 \approx *2$, so there is no $G'$ such that $G + G' \approx *0$.

Problem : Suppose we modify Coino (the coin flipping game from Homework #3) so that you get one do-over: at most once during the game you may discard the result of a flip and reflip any number of coins if the initial result was not to your liking. How would you modify the algorithm to find the optimal strategy and the expected winnings in this case?

Let the goal be $g$ and the inital number of coins be $s$. Denote by $E(c,t,r)$ the expected winnings given that the game has reached the position with $c$ coins left, $t$ total heads, and $r$ reflips available. Then $E(c,t,r) = 2.0$ when $t >= g$, and $E(c,t,r) = 0.0$ when $c = 0$ and $t < g$. For $0 < c < s$ and $0 \le t < g$ we have $$E(c,t,0) = \max_{1 \le f \le c} \left(\sum_{0 \le h \le {f \over 2}}^f P(h {\rm \ heads\ out\ of\ } f)*E(c-f,t+h,0) + \sum_{{f \over 2} < h \le f} P(h {\rm \ heads\ out\ of\ } f)*E(c,t+h,0) \right)$$ as before, and $$E(c,t,1) = \max_{1 \le f \le c} \left(\sum_{0 \le h \le {f \over 2}}^f P(h {\rm \ heads\ out\ of\ } f)*\max(E(c,t,0), E(c-f,t+h,1)) + \sum_{{f \over 2} < h \le f} P(h {\rm \ heads\ out\ of\ } f)*\max(E(c,t,0),E(c,t+h,1)) \right)$$ where the inner maxes represent the option of taking the result of a flip or using the reflip.

$OPT(c,t,r)$ would record the argmax of the outer max for each entry to record the optimal choices of how many coins to flip; $OPT(c,t,r,f,h)$ would store the argmax of the inner max to record, for each position $(c,t,r)$, choice ($f$), and outcome of that choice ($h$), whether the optimal choice was to reflip or not.

Problem : Compute the minimax value of each node in the tree below. Squares represent max nodes and circles represent min nodes.

Minimax tree
Top-to-bottom, left-to-right, the minimax values are 7;6,7,4;9,6,9,7,6,7,4.

Problem : Show the operation of alpha-beta pruning on the tree shown below. Show the (alpha, beta) windows passed to each node as the tree is traversed, the values returned from each node, and which branches are pruned.

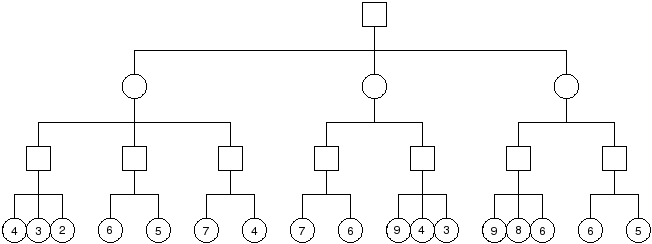
Alpha-beta tree
Labelling the nodes A through K top-to-bottom, left-to-right, the $(\alpha, \beta)$ windows passed to each node and the values returned are
Node$(\alpha, \beta)$Value
A $(-\infty, \infty)$ 7
B $(-\infty, \infty)$ 4
C $(4, \infty)$ 7
D $(7, \infty)$ 6
E $(-\infty, \infty)$ 4
F $(-\infty, 4)$ [prunes 2nd child] 6
G $(-\infty, 4)$ [prunes 2nd child] 7
H $(4, \infty)$ 7
I $(4, 7)$ [prunes 2nd, 3rd children] 9
J $(7, \infty)$ 9
K $(7, 9)$ 6

Problem : Repeat the previous exercise for Scout.

Labelling the nodes A through K top-to-bottom, left-to-right, the $(\alpha, \beta)$ windows passed to each node (nodes that are examined multiple times are given with each window passed to them and each returned value) and the values returned are
Node$(\alpha, \beta)$Value
A $(-\infty, \infty)$ 7
B $(-\infty, \infty)$ 4
C $(4, 5)$
$(5, \infty)$		 7
7
D $(7, 8)$ 6
E $(-\infty, \infty)$ 4
F $(-\infty, 4)$ [prunes 2nd child] 6
G $(-\infty, 4)$ [prunes 2nd child] 7
H $(4, 5)$ [prunes 2nd child]
$(5, \infty)$		 7
7
I $(4, 5)$ [prunes 2nd, 3rd children]
$(6, 7)$ [prunes 2nd, 3rd children]		 9
9
J $(7, 8)$ [prunes 2nd, 3rd children] 9
K $(7, 8)$ 6
This is from the version of Scout that calls Alpha-Beta with its first call.

Problem : Consider a constant-sum game with payoff matrix $$\left( \begin{array}{ccc} 0 & 2 & -1 \\ 1 & -2 & 0 \\ -2 & 0 & 2 \end{array} \right)$$.

Problem : Find a saddle point and its value for the constant-sum game with payoff matrix $$ \left( \begin{array}{cc} 3 & 2 \\ 0 & 4 \\ \end{array} \right) $$

The inequalities for $X$ are \begin{array}{rcccl} E(X, 1) & = & 3x & \ge & v \\ E(X, 2) & = & 4-2x & \ge & v \\ \end{array} The maximum value of $v$ that is below both lines is at their intersection, which is where $3x = 4 - 2x$, or $x = \frac{4}{5}$, so $X^* = (\frac{4}{5} \frac{1}{5})$.

For $Y$ the inequalities are \begin{array}{rcccl} E(1, Y) &=& y + 2 &\le& v \\ E(2, Y) &=& 4 - 4y &\le& v \\ \end{array} The minimum value of $v$ above both lines is at their intersection, which is where $y + 2 = 4 - 4y$, or $y = \frac{2}{5}$, so $Y^* = (\frac{2}{5} \frac{3}{5})$.

$E(X^*, Y^*) = \frac{12}{5}$.

Problem : Set up the linear program to find a saddle point for the constant-sum game with payoff matrix $$ \left( \begin{array}{ccc} 4 & 7 & 3 \\ 0 & 5 & 4 \\ 10 & 6 & 2 \\ \end{array} \right) $$

Minimize $p_1 + p_2 + p_3$ subject to \begin{array}{rcl} -5p_1 - p_2 - 11p_3 & \le & -1 \\ -8p_1 - 6p_2 - 7p_3 & \le & -1 \\ -4p_1 - 5p_2 - 3p_3 & \le & -1 \\ p_1, p_2, p_3 & \ge & 0 \\ p_1, p_2, p_3 & \le & 1 \\ \end{array}

Minimize $-q_1 - q_2 - q_3$ subject to \begin{array}{rcl} 5q_1 + 8q_2 + 4q_3 & \le & 1 \\ q_1 + 6q_2 + 5q_3 & \le & 1 \\ 11q_1 + 7q_2 + 3q_3 & \le & 1 \\ q_1, q_2, q_3 & \ge & 0 \\ q_1, q_2, q_3 & \le & 1 \\ \end{array}

Valid HTML 4.01 Transitional