Problem 0: Review old programming assignments, lectures, and readings. Use Piazza to suggest a question you feel is missing from this collection of practice problems. Draw a picture of the Code Mangler.
Problem : Comment on the quality of the two suggested hash functions for arrays of integers, considering the conditions that are required for hash table operations to work in $O(1)$ expected time.
Problem : Consider the problem of, given a list of integers, checking whether they are all different. Give an algorithm for this problem with an average case of $O(n)$ under reasonable assumptions. Give an algorithm that has a worst case $O(n \log n)$.
Problem : Suppose we have the following hash function:
| s | hash(s) |
|---|---|
| ant | 43 |
| bat | 23 |
| cat | 64 |
| dog | 19 |
| eel | 26 |
| fly | 44 |
| gnu | 93 |
| yak | 86 |
Problem :
Add the ismap_remove operation to the
implementation from Oct. 16
and modify the existing functions as necessary.
Problem : Draw the binary search tree that results from adding SEA, ARN, LOS, BOS, IAD, SIN, and CAI in that order. Find an order to add those that results in a tree of minimum height. Find an order to add those that results in a tree of maximum height. For your original tree, show the result of removing SEA, then show the order in which the nodes would be processed by an inorder traversal.
Problem : Repeat the original adds and delete from the previous problem for an AVL tree.
Problem : Repeat the original adds from the previous problem for a Red-Black tree.
Problem : Repeat the original adds and delete from the previous problem for a Splay tree using bottom-up splaying.
Problem :
Implement the expand operation for isset. The
expand operation takes an integer as its parameter and
expands the interval containing it to be as large as possible without
requiring a merge; it does not change the left endpoint or right endpoint
of the leftmost or rightmost interval in the tree respecitvely, and does
nothing if the integer is not in the set. For example, if a set
contains [3, 7], [10, 14], [20, 24], [90, 91] then expand(1)
would do nothing, expand(4) would change [3, 7] to [3, 8],
expand(22) would change [20, 24] into [16, 88], and
expand(90) would change [90, 91] into [26, 91].
Make sure your implementation runs in $O(\log n)$ time (worst case for AVL trees,
amortized for splay trees).
Problem :
Consider the remove_incoming operation, which takes a
vertex $v$ in a directed graph and removes all incoming edges to that
vertex. Explain how to implement remove_incoming when the
graph is represented using an adjacency matrix and then for an adjacency list.
What is the asymptotic running time of your implementations in terms of
the number of vertices $n$ and the total number of edges $m$?
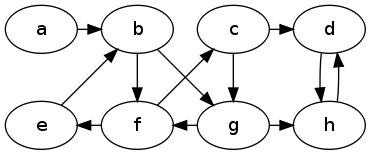
Problem : Show the DFS tree that results from running DFS on the following directed graph. Start at vertex $a$ and when you get to a vertex, consider its neighbors in alphabetical order.

Problem : Show the BFS tree that results from running BFS on the graph in the previous problem. Start at vertex $a$ and after dequeueing a vertex, consider its neighbors in alphabetical order.
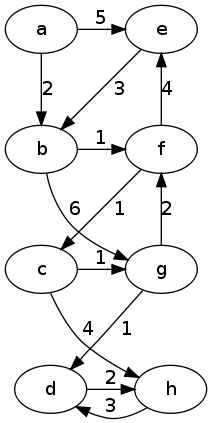
Problem : Illustrate the execution of Dijkstra's algorithm on the following graph, using a as the start vertex. Show the priorites before each dequeue operation and show the shortest paths tree at the end of the algorithm.
Problem : The following function computes $C(n,k)$, where $C(n, 0) = 1$ and $C(n, n) = 1$ for all $n \ge 0$, and $C(n, k) = C(n - 1, k - 1) + C(n - 1, k)$ for all $n, k$ such that $1 \le k \le n - 1$. ($C(n, k)$ is the number of distinct size-$k$ subsets of $\{1, \ldots, n\}$.
int choose(int n, int k)
{
if (k == 0 || n == k)
{
return 1;
}
else
{
int including_n = choose(n - 1, k - 1);
int not_including_n = choose(n - 1, k);
return including_n + not_including_n;
}
}
Problem : Write an efficient algorithm to determine how many different ways there are to make n cents change using pennies, nickels, dimes, and quarters (two collections of change are considered different if an only if they have a different number of pennies, a different number of nickels, a different number of dimes, or a different number of quarters).
Problem : Suppose a restaurant sells orders of pierogies in sizes $s_1, \ldots, s_k$ with costs $c_1, \ldots, c_k$. Give an efficient algorithm for determining the minimum cost to order $n$ pierogies total. (For example, if Yocco's sells pierogies in orders of size 1, 3, or 10 with corresponding costs 90 cents, $1.80, and $6.20 then the best way to order 11 pierogies total is to get a 1-pierogy order and a 10-pierogy order for a total cost of $7.10) What is the running time of your algorithm? What is the space requirement? Can you augment your algorithm to return the best way to order $n$ pierogies in addition to the corresponding cost?