Problem : Comment on the quality of the two suggested hash functions for arrays of integers, considering the conditions that are required for hash table operations to work in $O(1)$ expected time.
- the hash value is the bitwise exclusive-or of all the integers in the array
This is terrible! The hash value of an array of positive integers will always be between 0 and $2n$ where $n$ is the largest value in the array. There are many applications where there keys will be a large number of arrays with a small range and for those applications there will be many collisions, so worse than $O(1)$ expected time for operations on the hash table.
- the hash value is the sum of all the integers in the array
This is terrible! For arrays where the individual elements are uniformly distributed in some range, the sums will be clustered around half the range times the number of elements. That will lead to many collisions and so worse than $O(1)$ expected time for operations on the hash table.
Problem : Consider the problem of, given a list of integers, checking whether they are all different. Give an algorithm for this problem with an average case of $O(n)$ under reasonable assumptions. Give an algorithm that has a worst case $O(n \log n)$.
#include <stdio.h>
#include <stdbool.h>
#include "ismap.h"
#include "isset.h"
int hash(int x)
{
// from StackOverflow user Thomas Mueller
// https://stackoverflow.com/questions/664014/what-integer-hash-function-are-good-that-accepts-an-integer-hash-key
unsigned int z = x; // original was written for unsigned ints
z = ((z >> 16) ^ z) * 0x119de1f3;
z = ((z >> 16) ^ z) * 0x119de1f3;
z = (z >> 16) ^ z;
return (int)z;
}
bool distinct_with_hash(int intList[], int lenList, int (*hash)(int)){
//intList is the array of integers we are comparing.
//lenList is length of intList
//hash is an appropriate hash function
//assumes hash table implementation like in class.
ismap* hashmap = ismap_create(hash); //create the hashmap
int i = 0;
while (i < lenList && !ismap_contains_key(hashmap, intList[i]))
{
ismap_put(hashmap, intList[i], NULL);
i++;
}
ismap_destroy(hashmap);
return i == lenList;
}
bool distinct_with_tree(int intList[], int lenList){
//intList is the array of integers we are comparing.
//lenList is length of intList
//hash is an appropriate hash function
//assumes hash table implementation like in class.
isset* treeset = isset_create(); //create the hashmap
int i = 0;
while (i < lenList && !isset_contains(treeset, intList[i]))
{
isset_add(treeset, intList[i]);
i++;
}
isset_destroy(treeset);
return i == lenList;
}
int main()
{
int test_distinct[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
int test_not_distinct[] = {5, 4, 8, 33, 20, 22, 33}; // who knows the significance of these?
printf("Elements are distinct, return values are:\n");
printf("%d\n", distinct_with_hash(test_distinct, sizeof(test_distinct) / sizeof(test_distinct[0]), hash));
printf("%d\n", distinct_with_tree(test_distinct, sizeof(test_distinct) / sizeof(test_distinct[0])));
printf("Elements are not distinct, return values are:\n");
printf("%d\n", distinct_with_hash(test_not_distinct, sizeof(test_not_distinct) / sizeof(test_not_distinct[0]), hash));
printf("%d\n", distinct_with_tree(test_not_distinct, sizeof(test_not_distinct) / sizeof(test_not_distinct[0])));
}
Assuming proper sizing of the hash table in ismap
and a good hash function, each
contains_key and put in distinct_with_hash
runs in $\Theta(1)$ expected time; we call
them up to $n$ times for a total of $\Theta(n)$ expected time.
If the isset used in distinct_with_tree is implemented
with a balanced BST like an AVL tree or a Red-Black tree then each
contains and add
runs in $O(\log n)$ time; we call
them up to $n$ times for a total of $O(n \log n)$ worst-case time.
Sorting using a worst case $O(n \log n)$ sort and then searching for equal consecutive elements will also give $O(n \log n)$ time overall.
Problem : Suppose we have the following hash function:
| s | hash(s) |
|---|---|
| ant | 43 |
| bat | 23 |
| cat | 64 |
| dog | 19 |
| eel | 26 |
| fly | 44 |
| gnu | 93 |
| yak | 86 |
0: cat 1: 2: eel 3: ant dog 4: fly 5: gnu 6: yak 7: bat
0: cat 1: yak 2: eel 3: ant 4: dog 5: fly 6: gnu 7: bat
Problem :
Add the ismap_remove operation to the
implementation from Oct. 30
and modify the existing functions as necessary.
We indicate deleted slots leaving the occupied flag set and setting the value to a special
value deleted. Removing is then finding the slot containing the key and marking
it as deleted. The other functions need to be modified to skip over deleted slots.
char *ismap_deleted = "this can be anything; the important thing is that is won't ever be used as a legitimate value"; void ismap_remove(ismap *m, int key) { int index = ismap_table_find_key(m->table, key, m->hash, m->capacity, false); if(m->table[index].occupied) { m->table[index].value = ismap_deleted; m->size--; } } int ismap_table_find_key(const entry *table, int key, int (*hash)(int), int capacity, bool insert) { // compute starting location for search from hash function int i = ismap_compute_index(key, hash, capacity); int first_deleted = (table[i].occupied && table[i].value == ismap_deleted) ? i : -1; while (table[i].occupied && table[i].key != key) { // remember the index of the first deleted slot so we can back up to it if necessary if((table[i].value == ismap_deleted) && (first_deleted == -1)) { first_deleted = i; } i = (i + 1) % capacity; } // return the index of the first deleted slot we encountered if finding one to insert in if(insert && !table[i].occupied && first_deleted != -1) { return first_deleted; } return i; } void ismap_put(ismap *m, int key, char *value) { int index = ismap_table_find_key(m->table, key, m->hash, m->capacity, true); if (m->table[index].occupied) { if (m->table[index].value == ismap_deleted) { // reusing a deleted slot m->table[index].key = key; m->size++; } // else key already present m->table[index].value = value; } else { if (m->size + 1 > m->capacity / 2) { // grow ismap_embiggen(m); // add to table if (m->size + 1 < m->capacity) { // need add here since the index of the free spot will // have changed after rehashing ismap_table_add(m->table, key, value, m->hash, m->capacity); m->size++; } } else { // add to table at free spot we found m->table[index].key = key; m->table[index].value = value; m->table[index].occupied = true; m->size++; } } } bool ismap_contains_key(const ismap *m, int key) { int i = ismap_table_find_key(m->table, key, m->hash, m->capacity, false); return (m->table[i].occupied && m->table[i].value != ismap_deleted); } char *ismap_get(ismap *m, int key) { int index = ismap_table_find_key(m->table, key, m->hash, m->capacity, false); if (m->table[index].occupied && (m->table[index].value != ismap_deleted)) { return m->table[index].value; } else { return NULL; } } void ismap_for_each(ismap *m, void (*f)(int, char *)) { for (int i = 0; i < m->capacity; i++) { if (m->table[i].occupied && m->table[i].value != ismap_deleted) { f(m->table[i].key, m->table[i].value); } } } void ismap_for_each_r(ismap *m, void (*f)(int, char *, void *), void *arg) { for (int i = 0; i < m->capacity; i++) { if (m->table[i].occupied && m->table[i].value != ismap_deleted) { f(m->table[i].key, m->table[i].value, arg); } } }
Problem : Draw the binary search tree that results from adding SEA, ARN, LOS, BOS, IAD, SIN, and CAI in that order.
SEA
/ \
ARN SIN
\
LOS
/
BOS
\
IAD
/
CAI
Find an order to add those that results in a tree of minimum height.
IAD, BOS, ARN, CAI, SEA, LOS, SIN
Find an order to add those that results in a tree of maximum height.
Find an order to add those that results in a tree of maximum height.
SIN, SEA, ARN, LOS, BOS, IAD, CAI
For your original tree, show the result of removing SEA, then show the order in which the nodes would be processed by an inorder traversal.
SIN
/
ARN
\
LOS
/
BOS
\
IAD
/
CAI
or
LOS
/ \
ARN SIN
\
BOS
\
IAD
/
CAI
ARN, BOS, CAI, IAD, LOS, SIN
Problem : Repeat the original adds and delete from the previous problem for an AVL tree.
LOS
/ \
BOS SEA
/ \ \
ARN IAD SIN
/
CAI
After all deletes:
IAD
/ \
BOS LOS
/ \ \
ARN CAI SIN
Problem : Repeat the original adds from the previous problem for a Red-Black tree.
LOS
/ \
BOS SEA
/ \ \
ARN IAD SIN
/
CAI
Problem : Repeat the original adds and delete from the previous problem for a Splay tree using bottom-up splaying.
CAI
/ \
BOS SIN
/ /
ARN IAD
\
SEA
/
LOS
After deleting by splaying node to delete, deleting at root, splaying largest node of left subtree, joining left & right subtree:
LOS
/ \
IAD SIN
/
CAI
/
BOS
/
ARN
After deleting by swapping with inorder predecessor and splaying parent:
IAD
/ \
CAI SIN
/ /
BOS LOS
/
ARN
Problem :
Implement the expand operation for isset. The
expand operation takes an integer as its parameter and
expands the interval containing it to be as large as possible without
requiring a merge; it does not change the left endpoint or right endpoint
of the leftmost or rightmost interval in the tree respecitvely, and does
nothing if the integer is not in the set. For example, if a set
contains [3, 7], [10, 14], [20, 24], [90, 91] then expand(1)
would do nothing, expand(4) would change [3, 7] to [3, 8],
expand(22) would change [20, 24] into [16, 88], and
expand(90) would change [90, 91] into [26, 91].
Make sure your implementation runs in $O(\log n)$ time (worst case for AVL trees,
amortized for splay trees).
bool isset_expand(isset *s, int item, int *start, int *end)
{
if (s == NULL)
{
return false;
}
isset_search_result result;
isset_find_node(s, item, &result);
if (result.found)
{
// find inorder predecessor
isset_node *pred;
bool had_left = false;
if (result.n->left == NULL)
{
pred = result.last_right;
}
else
{
had_left = true;
for (pred = result.n->left; pred->right != NULL; pred = pred->right);
}
// update start to get as close as possible to predecessor w/o merge
if (pred != NULL)
{
int new_start = pred->end + 2;
s->size += (result.n->start - new_start);
result.n->start = new_start;
}
// find inorder successor
isset_node *succ;
bool had_right = false;
if (result.n->right == NULL)
{
succ = result.last_left;
}
else
{
had_right = true;
for (succ = result.n->right; succ->left != NULL; succ = succ->left);
}
// update end to get as close as possible to successor w/o merge
if (succ != NULL)
{
int new_end = succ->start - 2;
s->size += (new_end - result.n->end);
result.n->end = new_end;
}
// return new interval
*start = result.n->start;
*end = result.n->end;
// we may have gone down two branches; splay at the bottom of _both_
if (!had_left && !had_right)
{
isset_splay(s, result.n);
}
else
{
if (had_left)
{
isset_splay(s, pred);
}
if (had_right)
{
isset_splay(s, succ);
}
}
return true;
}
else
{
isset_splay(s, result.parent);
return false;
}
}
Problem :
Consider the remove_incoming operation, which takes a
vertex $v$ in a directed graph and removes all incoming edges to that
vertex. Explain how to implement remove_incoming when the
graph is represented using an adjacency matrix and then for an adjacency list.
What is the asymptotic running time of your implementations in terms of
the number of vertices $n$ and the total number of edges $m$?
For an adjacency matrix: set all entries in the column for vertex
$v$ to false. This will take $\Theta(V)$ time.
for each vertex u use sequential search to find v on u's adjacency list if found, deleteThis will take $\Theta(V+E)$ time since in we iterate over all entries in the adjacency lists (worst case if the adjacency lists are linked lists because we can stop when we find $v$; every case if the adjacency lists are arrays and we want to preserve the order of the adjacency list : we would go through the array to find $v$ and then go through the rest of the array to move elements back to fill the hole created when $v$ was removed).
Problem : Show the DFS tree that results from running DFS on the following directed graph. Start at vertex $a$ and when you get to a vertex, consider its neighbors in alphabetical order.
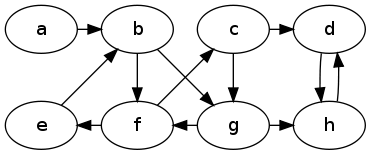
a
|
b
|
f
/ \
c e
/ \
d g
|
h
Problem : Show the BFS tree that results from running BFS on the graph in the previous problem. Start at vertex $a$ and after dequeueing a vertex, consider its neighbors in alphabetical order.
a
|
b
/ \
f g
/ \ \
c e h
|
d
Problem : The following function computes $C(n,k)$, where $C(n, 0) = 1$ and $C(n, n) = 1$ for all $n \ge 0$, and $C(n, k) = C(n - 1, k - 1) + C(n - 1, k)$ for all $n, k$ such that $1 \le k \le n - 1$. ($C(n, k)$ is the number of distinct size-$k$ subsets of $\{1, \ldots, n\}$.
int choose(int n, int k)
{
if (k == 0 || n == k)
{
return 1;
}
else
{
int including_n = choose(n - 1, k - 1);
int not_including_n = choose(n - 1, k);
return including_n + not_including_n;
}
}
- Explain why this code is inefficient.
There are many overlapping subproblems. For example,
choose(6, 4)callschoose(5, 4)andchoose(5,3). Both of those callchoose(4,3). - Write more efficient code to compute $C(n, k)$. What is running time
of your code in terms of $n$ and $k$? What is the space requirement?
Can you reduce the space requirement to $\Theta(n)$ (if you are not
there already)?
double choose1(int n, int k){ // Use dynamic programming to calculate choose(n,k). // when computing row n, we only need the values in row n-1, // so instead of keeping the entire 2-D array, we just // keep the previous row. double prevRow[n]; for(int i = 0; i < n; i++){ prevRow[i] = 1.0; //set all values in prevRow to 1.0 to start. } int i = 0; while(i < n){ // prevRow holds values of choose(i, k) i++; //get the index of the next row to compute. //allocate space for current row. double currRow[n]; //use base cases to initialize first and last value. currRow[0] = 1; currRow[i] = 1; //use the general case to compute the rest of the value for(int j = 1; j < i; j++){ currRow[j] = prevRow[j-1] + prevRow[j]; } //the current row becomes the previous row for the next iteration for(int j = 0; j < i; j++){ prevRow[j] = currRow[j]; } } //get the value we want out of the last row computer (row n). return prevRow[k]; } int main() { int n = 10; int k = 8; unsigned long long result1 = choose1(n,k); printf("With recursion: %llu\n",result1); }This runs in time $\Theta(n^2)$ and space $\Theta(n)$ – can you reduce it to time $\Theta(nk)$? (Note that you can write even more efficient code that uses the formula $C(n, k) = \frac{n!}{k!(n-k)!}$ – see below.)unsigned long long choose2(int n, int k) { //calculate choose(n,k) using factorials. //this will probably overflow and give garbage results -- can you //modify it so it is less likely to overflow? //i.e. choose(n,k) = n!/k!/(n-k)! unsigned long long nFactorial = 1; //n! unsigned long long kFactorial = 1; //k! unsigned long long nkFactorial = 1; //(n-k)! int i; for(i = 2; i < n+1; i++){ nFactorial = nFactorial*i; } for(i = 2; i < k+1; i++){ kFactorial = kFactorial*i; } for(i = 2; i < n-k+1; i++){ nkFactorial = nkFactorial*i; } return nFactorial/(kFactorial*nkFactorial); }