Solutions to Exam #2 Practice

Problem : Comment on the quality of the two suggested hash functions for arrays of integers, considering the conditions that are required for hash table operations to work in $O(1)$ expected time.

the hash value is the bitwise exclusive-or of all the integers in the array
This is terrible! The hash value of an array of positive integers will always be between 0 and $2n$ where $n$ is the largest value in the array. There are many applications where there keys will be a large number of arrays with a small range and for those applications there will be many collisions, so worse than $O(1)$ expected time for operations on the hash table.
the hash value is the sum of all the integers in the array
This is terrible! For arrays where the individual elements are uniformly distributed in some range, the sums will be clustered around half the range times the number of elements. That will lead to many collisions and so worse than $O(1)$ expected time for operations on the hash table.

Problem : Consider the problem of, given a list of integers, checking whether they are all different. Give an algorithm for this problem with an average case of $O(n)$ under reasonable assumptions. Give an algorithm that has a worst case $O(n \log n)$.

#include <stdio.h>
#include <stdbool.h>

#include "ismap.h"
#include "isset.h"

int hash(int x)
{
  // from StackOverflow user Thomas Mueller
  // https://stackoverflow.com/questions/664014/what-integer-hash-function-are-good-that-accepts-an-integer-hash-key
  unsigned int z = x; // original was written for unsigned ints
  z = ((z >> 16) ^ z) * 0x119de1f3;
  z = ((z >> 16) ^ z) * 0x119de1f3;
  z = (z >> 16) ^ z;
  return (int)z;
}
  
bool distinct_with_hash(int intList[], int lenList, int (*hash)(int)){
  //intList is the array of integers we are comparing.
  //lenList is length of intList
  //hash is an appropriate hash function
  //assumes hash table implementation like in class.
  
  ismap* hashmap = ismap_create(hash); //create the hashmap

  int i = 0;
  while (i < lenList && !ismap_contains_key(hashmap, intList[i]))
      {
	ismap_put(hashmap, intList[i], NULL);
	i++;
      }
  ismap_destroy(hashmap);
  
  return i == lenList;
}

bool distinct_with_tree(int intList[], int lenList){
  //intList is the array of integers we are comparing.
  //lenList is length of intList
  //hash is an appropriate hash function
  //assumes hash table implementation like in class.
  
  isset* treeset = isset_create(); //create the hashmap

  int i = 0;
  while (i < lenList && !isset_contains(treeset, intList[i]))
      {
	isset_add(treeset, intList[i]);
	i++;
      }
  isset_destroy(treeset);
  
  return i == lenList;
}

int main()
{
  int test_distinct[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16};
  int test_not_distinct[] = {5, 4, 8, 33, 20, 22, 33}; // who knows the significance of these?

  printf("Elements are distinct, return values are:\n");
  printf("%d\n", distinct_with_hash(test_distinct, sizeof(test_distinct) / sizeof(test_distinct[0]), hash));
  printf("%d\n", distinct_with_tree(test_distinct, sizeof(test_distinct) / sizeof(test_distinct[0])));
  printf("Elements are not distinct, return values are:\n");
  printf("%d\n", distinct_with_hash(test_not_distinct, sizeof(test_not_distinct) / sizeof(test_not_distinct[0]), hash));
  printf("%d\n", distinct_with_tree(test_not_distinct, sizeof(test_not_distinct) / sizeof(test_not_distinct[0])));
}

Assuming proper sizing of the hash table in ismap and a good hash function, each contains_key and put in distinct_with_hash runs in $\Theta(1)$ expected time; we call them up to $n$ times for a total of $\Theta(n)$ expected time.

If the isset used in distinct_with_tree is implemented with a balanced BST like an AVL tree or a Red-Black tree then each contains and add runs in $O(\log n)$ time; we call them up to $n$ times for a total of $O(n \log n)$ worst-case time.

Sorting using a worst case $O(n \log n)$ sort and then searching for equal consecutive elements will also give $O(n \log n)$ time overall.

Problem : Suppose we have the following hash function:

s	hash(s)
ant	43
bat	23
cat	64
dog	19
eel	26
fly	44
gnu	93
yak	86

Show the results of adding the strings in alphabetical order into a hash table of size 8, first using chaining, then using open addressing with linear probing.

0: cat
1:
2: eel
3: ant dog
4: fly
5: gnu
6: yak
7: bat

0: cat
1: yak
2: eel
3: ant
4: dog
5: fly
6: gnu
7: bat

Problem : Write pseudocode for a non-recursive version of an inorder traversal of a binary search tree. (Hint: for any node, where is the node with the next highest value?)

start at the leftmost node
while there is a current node
- process that node
- if the current node has a right child, set the next node to the leftmost node in the right subtree
- otherwise, set the next node to deepest ancestor of the current node so that the path from that ancestor to the current node follows a left branch (back up the tree until you've backed up a left branch)
- set the current node to be the next node

Problem : Draw the binary search tree that results from adding SEA, ARN, LOS, BOS, IAD, SIN, and CAI in that order.

          SEA
        /     \
    ARN         SIN
       \
        LOS
       /
    BOS
       \
         IAD
       /
    CAI

Find an order to add those that results in a tree of minimum height.

IAD, BOS, ARN, CAI, SEA, LOS, SIN

Find an order to add those that results in a tree of maximum height.

SIN, SEA, ARN, LOS, BOS, IAD, CAI

For your original tree, show the result of removing SEA, then show the order in which the nodes would be processed by an inorder traversal.

          SIN
        /    
    ARN 
       \
        LOS
       /
    BOS
       \
         IAD
       /
    CAI

          LOS
        /     \
    ARN         SIN
       \
        BOS
           \
            IAD
           /
        CAI

ARN, BOS, CAI, IAD, LOS, SIN

Problem : Repeat the original adds and delete from the previous problem for an AVL tree.

After all adds:

            LOS
        /         \
      BOS          SEA
    /     \          \
  ARN        IAD       SIN
            /
         CAI

After all deletes:

         IAD
      /       \
  BOS           LOS
 /   \              \
ARN   CAI             SIN

Problem : Repeat the original adds from the previous problem for a Red-Black tree.

After all adds:

            LOS
         /       \
      BOS          SEA
    /     \          \
  ARN        IAD       SIN
            /
         CAI

Problem : Consider the remove_incoming operation, which takes a vertex $v$ in a directed graph and removes all incoming edges to that vertex. Explain how to implement remove_incoming when the graph is represented using an adjacency matrix and then for an adjacency list. What is the asymptotic running time of your implementations in terms of the number of vertices $n$ and the total number of edges $m$?

For an adjacency matrix: set all entries in the column for vertex $v$ to false. This will take $\Theta(n)$ time.

For adjacency lists:

for each vertex u
  use sequential search to find v on u's adjacency list
  if found, delete

This will take $\Theta(n+m)$ time since in we iterate over all entries in the adjacency lists (worst case if the adjacency lists are linked lists because we can stop when we find $v$; every case if the adjacency lists are arrays and we want to preserve the order of the adjacency list : we would go through the array to find $v$ and then go through the rest of the array to move elements back to fill the hole created when $v$ was removed).

Problem : Show the result of running breadth-first search on the following directed graph. Start at vertex $a$ and after dequeueing a vertex, consider its neighbors in alphabetical order.

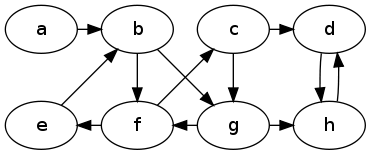
Predecessor relationships are shown in tree form, so that if pred[v] = u then v is a child of u in the tree

d=0      a
         |
d=1      b
        / \  
d=2    f   g
      / \   \
d=3  c   e   h
     |
d=4  d

Problem : Show the result of running depth-first search on the graph in the previous problem. Start at vertex $a$ and when you get to a vertex, consider its neighbors in alphabetical order.

    a
    |
    b
    | 
    f   
   / \
  c   e
 / \
d  g
|
h

Problem : Show the operation of heapsort when starting with the array [8, 4, 6, 9, 1, 3, 7]. Show the steps in both the build phase and the sort phase.

This shows the version of heapsort that uses heap_reheap_down in the first step.