Notes:
- Algorithms should be given in pseudocode. Please try to avoid
relying on features of particular programming languages
that would be unfamiliar to readers unfamiliar with that
programming language (for example, negative indices in Python
or the Python
itertoolslibrary). - For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
- "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."
- Note that you can view source to see the LaTeX source for most of the formulas.
Problem : Complete the Canvas quizzes on greedy algorithms and multi-modal shortest paths.
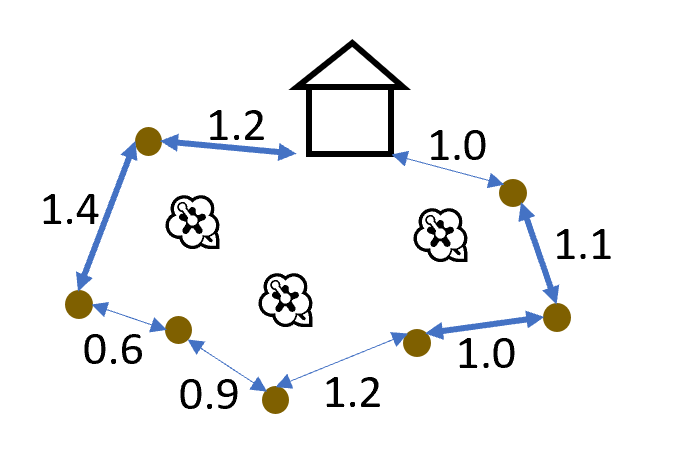
Problem : Prof. and Mrs. Glenn need to build a fence around their yard to keep the deer from eating their azaleas. The fence will start at one corner of their house and end at another. The perimeter of their yard is marked by trees, and the fence must follow that perimeter. Furthermore, the fencing is sold in lengths of $L$ and, to avoid setting fenceposts, each segment of fencing must start and end at either a corner of the house or a tree; the next segment then starts at the tree where the previous segment ended. Segments less than $L$ are possible, but the scraps may not be reused in other parts of the fence.
Devise a $\Theta(n)$ algorithm to determine the minimum number of fencing segments the Glenns must buy to complete their fence, and prove that your algorithm is correct. The inputs should be as follows:
- $d$, a non-empty list of the strictly increasing distances along the perimeter of the yard to each tree in increasing order, starting with 0.0 for the first corner of the house, with no two consecutive elements more than $L$ apart, and ending with the total length of the perimeter;
- $L$, the length of the segments of fencing; and
- $n$, the number of trees along the perimeter (so the number of elements in $d$ is $n + 2$).
You may use a simple sequential search as
part of your algorithm without proving that the sequential search
is correct (although that is a good exercise).
Problem : Consider the following job scheduling problem. We are given all at once $n$ jobs with positive lengths $t_1, t_2, \ldots, t_n$ and positive weights $w_1, \ldots, w_n$. We can schedule only one job at a time and once we start a job we must run it to completion. A schedule for a set of jobs is then the starting time for each job $s_1, s_2, \ldots, s_n$. Find an efficient algorithm to find a schedule of the jobs to minimize the total weighted turnaround time, where the turnaround time for a job is the difference between the time the job arrived and when it finished. Since all jobs arrive at the same time $t=0$, the turnaround time for job $i$ simplifies to $s_i + t_i$ and so the problem is to schedule the jobs to minimize $\sum_{i=1}^n w_i\cdot (s_i + t_i)$. Prove that your algorithm is correct (if you use a greedy algorithm you need only prove that the solution resulting from your greedy choice is always optimal, not that your algorithm correctly finds that greedy solution).
Problem : Devise an efficient algorithm for determining the location of food deserts. The input is
- an undirected, connected, weighted graph $G$ with vertices $1, \ldots, n$; this graph represents a sparse street network ($m \in \Theta(n)$), where the vertices are intersections and the weights are distances between the intersections;
- an array $pop$ where $pop[i]$ gives the population at each intersection (for simplicity we imagine people living at the intersections instead of along the edges);
- a non-empty list $S$ of the intersections where a sufficient variety of nutritious foods can be purchased, and $k$, the length of that list (there may be non-zero population at those intersections too);
- $b$, which defines our notion of what a food desert is: for each intersection we find the shortest path to any intersection in $S$. Any intersection that is strictly farther away from all intersections in $S$ than the $b$ closest people are considered to be in a food desert.
The output should be a list of the intersections that are food deserts. Compute the asymptotic running time of your algorithm, explaining your computation. Include in your explanation your choice of representation for the graph and other ADTs used in your solution. You need not prove that your algorithm is correct.
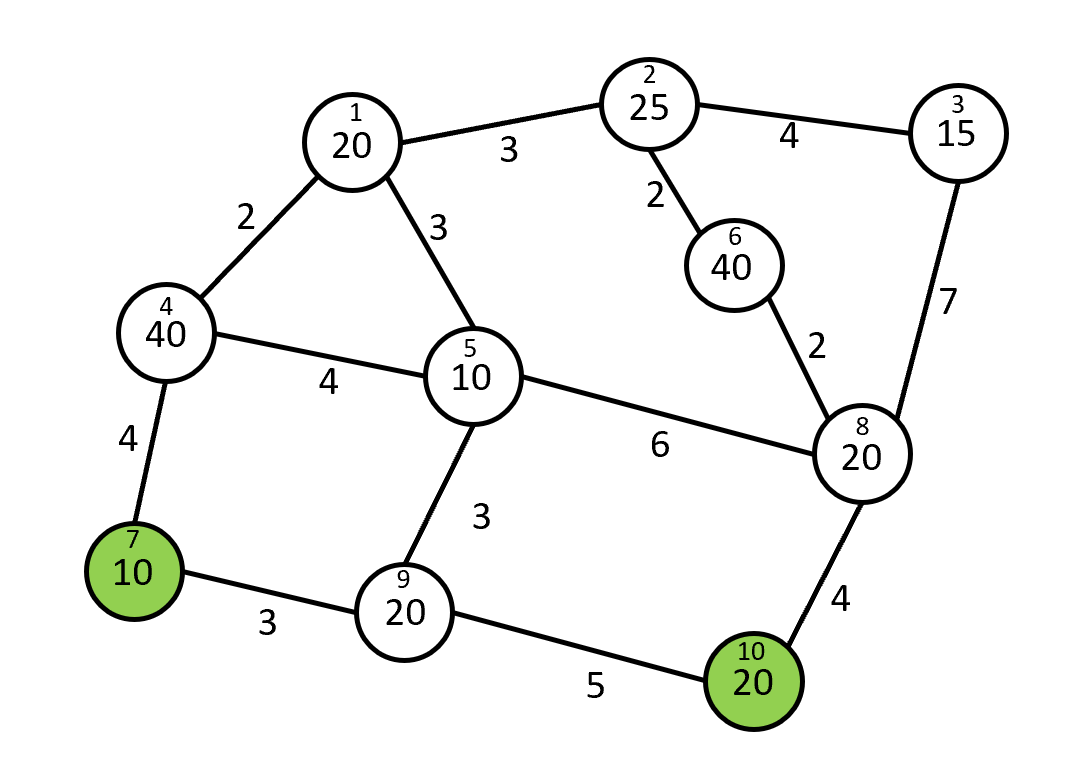
| Vertex | Closest Food | Dist. | Pop. | Cumulative Pop. |
|---|---|---|---|---|
| 7 | 7 | 0 | 10 | 10 |
| 10 | 10 | 0 | 20 | 30 |
| 9 | 7 | 3 | 20 | 50 |
| 4 | 7 | 4 | 40 | 90 |
| 8 | 10 | 4 | 20 | 110 |
| 5 | 7 | 6 | 10 | 120 |
| 1 | 7 | 6 | 20 | 140 |
| 6 | 10 | 6 | 40 | 180 |
| 2 | 10 | 8 | 25 | 205 |
| 3 | 10 | 11 | 15 | 220 |
The small number in each vertex is its index; the large number is its population. The table shows vertices sorted by distance to closest food source, with cumulative population. $S$ is $[7, 10]$. When $b = 130$, the output would be $[2, 3]$ or $[3, 2]$ since the closest 130 people live within 6 or closer of an intersection in $S$ and the people who live at $2$ and $3$ are strictly farther than that (8 and 11 respectively). Note that the people at vertex 6 are at the same distance as those at vertices 1 and 5, so they are not in a food desert – the "strictly farther" condition disambiguates cases like this where reordering vertices that are all at the threshold distance (5, 1, and 6 in this example) would result in different sets containing the closest $b$.