Notes:

• Algorithms should be given in pseudocode. Please try to avoid relying on features of particular programming languages that would be unfamiliar to readers unfamiliar with that programming language (for example, negative indices in Python or the Python itertools library).
• For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
• "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."
• Note that you can view source to see the LaTeX source for most of the formulas.

---

Problem : Complete the Canvas quiz on minimum spanning trees.

Problem : Give an $O(m \log n)$ algorithm to determine if a given minimum spanning tree is unique. The inputs to your algorithm are

• $n$, the number of vertices in the graph (the vertices are then numbered $0, \ldots, n-1$);
• the set of edges in the graph and their weights, as an adjacency list or adjacency matrix (specify which one you are using);
• a subset $T$ of the edges that forms a minimum spanning tree, using the same data structure as the complete set of edges.

You may assume that 1) if the given $T$ is not the unique minimum spanning tree then there is another minimum spanning tree $T'$ that differs from it by one edge; and 2)you can determine the edge of maximum weight (and its weight) on the simple path between any two vertices using edges in $T$ in $O(\log n)$ time. Compute the overall asymptotic running time of your algorithm in terms of $n$ (the number of vertices) and $m$ (the number of edges) and explain your result. You need not prove that your algorithm is correct.

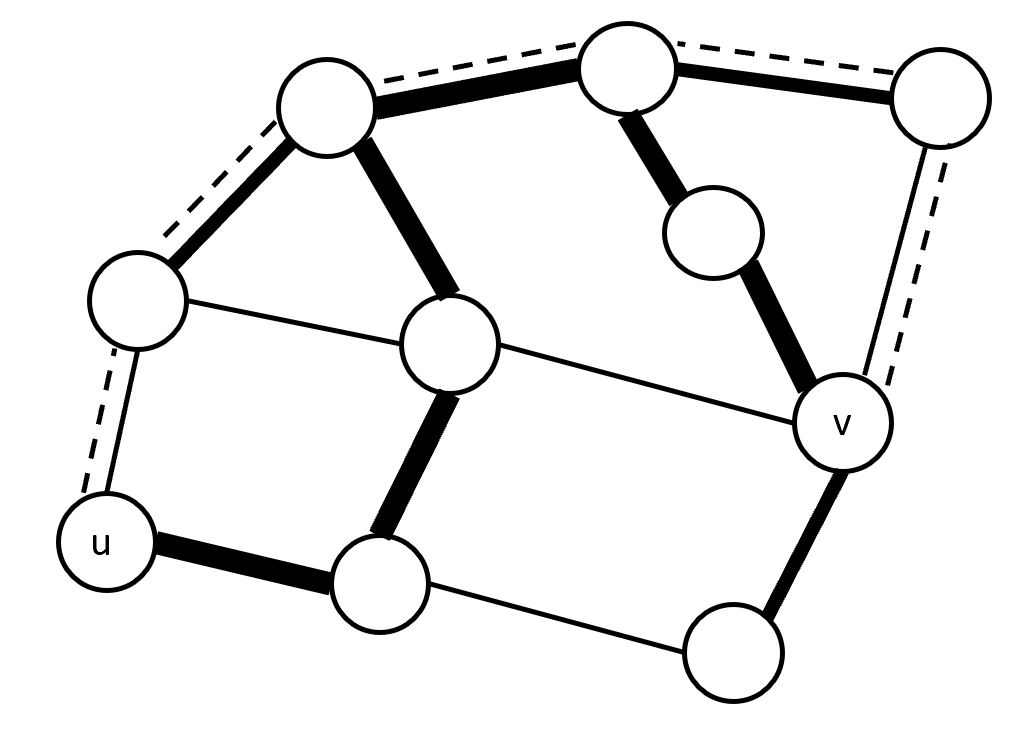
Problem : Prove that for any minimum spanning tree $T$ for a connected, undirected graph $G$ with positive (and not necessarily distinct) egde weights, and for any pair of vertices $u, v$, and any path $P$ from $u$ to $v$ in $G$, the maximum weight edge along $P$ has a weight that is at least as high as the maximum weight edge along the unique simple path from $u$ to $v$ in $T$.