Notes:

• For this class is is generally not necessary to validate input in your pseudocode: if a problem says the input will be in a certain form then write your pseudocode under the assumption that the input is in that form.
• "Find/devise/give an efficient algorithm" means "find an algorithm that is as efficient as possible, and you have to figure out for yourself whether your solution can be improved."

Problem : Complete the Canvas quiz on P vs. NP.

Problem : We can define co-NP-complete just like NP-complete: a problem $X$ is co-NP-complete if a) $X \in co-NP$, and b) for all $Y \in co-NP$, $Y \le_P X$. Show that if there is a co-NP-complete problem $X$ such that $X \in P$ then $P = NP$.

Problem : HAMILTONIAN-PATH (HP: the problem of, given an undirected graph $G$, determining whether $G$ has a Hamiltonian path) is NP-complete. But perhaps the problem becomes easier if we relax the requirements somewhat. Consider BURRIAN-PATH, which is the problem of, given an undirected, connected graph $G$, determining if $G$ has a simple path that visits at least $\Bigl\lfloor \frac{n}{2} \Bigr\rfloor$ vertices. Prove that this modified problem is not in fact any easier in some sense: BURRIAN-PATH is NP-complete. Give the same level of detail as in the $HC \le_P HP$ video when showing that things that need to be polynomial-time and polynomial-size are polynomial-time and polynomial-size.

Problem :

The FIND-FEEDBACK-ARC-SET problem ($FFAS$) is the problem of, given a directed graph, finding the smallest subset $S$ of the edges such that removing $S$ makes the graph acyclic. For example, the following graph has cycles UNC, FSU, Duke, UNC and UNC, Wake, FSU, Duke, UNC.

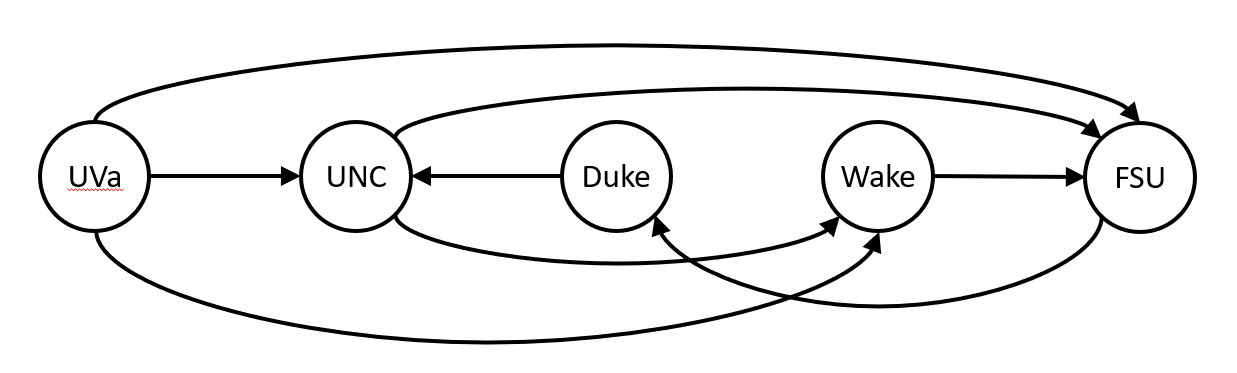
But removing the edges from UNC to FSU and from Wake to FSU breaks both of those cycles.

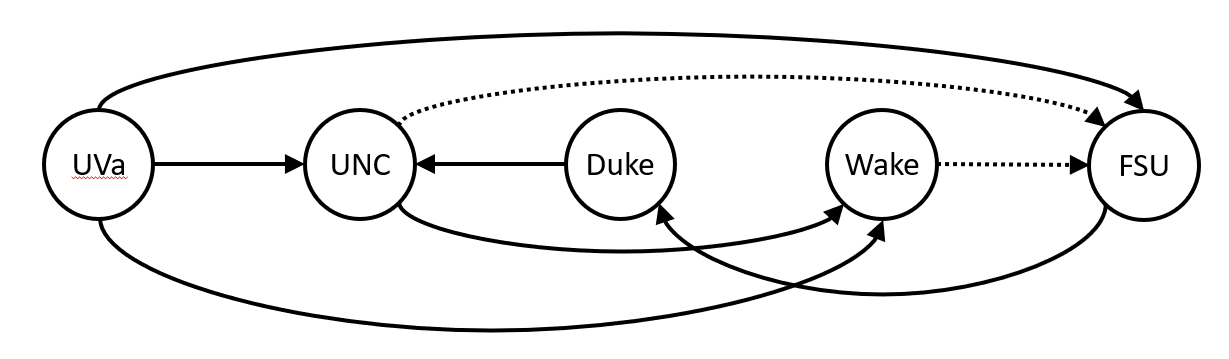
However, there is also a single edge that, when removed, leaves an acyclic graph.

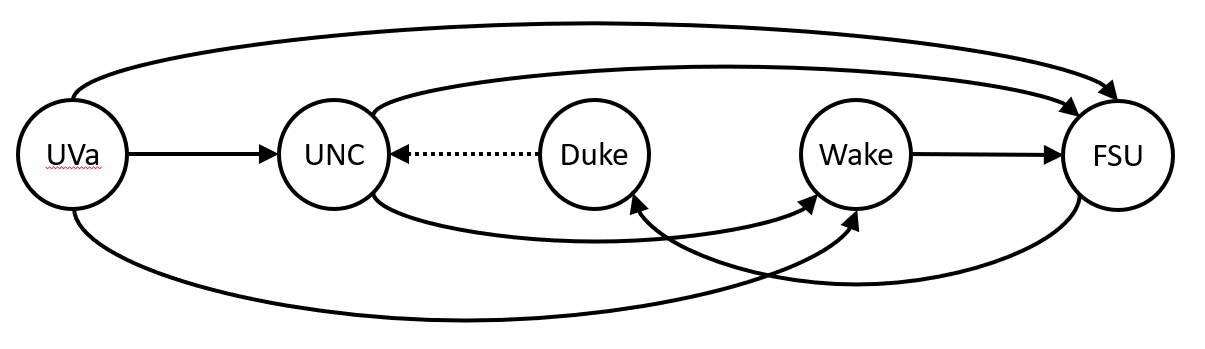
We can now move the vertices around so that all of the edges, except the edge from Duke to UNC, go left to right.

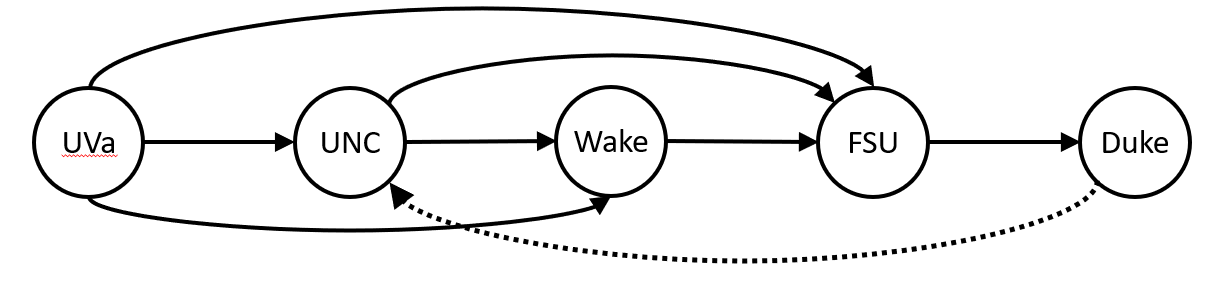
This illustrates that $FFAS$ is equivalent to the problem of ordering the vertices from left to right to minimize the number of edges that go right to left – removing those wrong-way edges would make the graph acyclic.

The graphs shown above reflect the results of a sequence of head-to-head matches between teams: the vertices represent teams and there is an edge from team A to team B if A beat B head-to-head. A minimum feedback arc set corresponds to a ranking that minimizes the number of upsets (results where a team listed earlier in the ranking lost to a team listed later).

In addition to sports, $FFAS$ has applications in many other areas, including graph visualization, clearing misinformation from social networks, and economics.

$FFAS$ is a search problem. The correspondng decision problem FEEDBACK-ARC-SET ($FAS$) is the problem of, given a directed graph $G$ and an integer $k$, determining whether there is a subset of edge $S$ of size at most $k$ such that deleting the edges in $S$ results in an acyclic graph.

Show that $FAS$ and $FFAS$ are in some sense equivalently difficult: there is a polynomial time algorithm for $FFAS$ if and only if there is a polynomial time algorithm for $FAS$. Prove this by showing that a) $FAS \le_P FFAS$ (write a polynomial-time algorithm for $FAS$ using a polynomial-time algorithm that solves $FFAS$ as a subrouti); and use of that subroutine as 1 step); and b) $FFAS \le_P FAS$ (write a polynomial-time algorithm for $FFAS$ using a polynomial-time algorithm that solves $FAS$ as a subroutine). In both cases, you needn't prove that your algorithm is correct, but you should explain why the running times are polynomial assuming that the required polynomial-time subroutine exists.