YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 461b: Foundations of Cryptography | Notes 7 (rev. 1) |
| Professor M. J. Fischer | | February 3, 2009 |
|
|
|
| |
19 Strongly One-Way from Weakly One-Way Functions
We now complete the proof theorem 1 from lecture 6 by constructing a strongly one-way function g from
a weakly one-way function f.
Let f be a weakly one-way function with associated polynomial p(⋅). Assume w.l.o.g. that f is
length-preserving. Let t(n) = n ⋅ p(n), and let T = {n ⋅ t(n)∣n  ℕ}. Let g be the function on length
n⋅t(n) strings defined by g(x1,…,xt(n)) = (f(x1),…,f(xt(n)), where |x1|,…,|xt(n)| = n. That is, given a
string x of length n ⋅ t(n), g splits it into t(n) length-n strings x1,…,xt(n), applies f(⋅) to each, and
concatenates the t(n) result strings so obtained.
ℕ}. Let g be the function on length
n⋅t(n) strings defined by g(x1,…,xt(n)) = (f(x1),…,f(xt(n)), where |x1|,…,|xt(n)| = n. That is, given a
string x of length n ⋅ t(n), g splits it into t(n) length-n strings x1,…,xt(n), applies f(⋅) to each, and
concatenates the t(n) result strings so obtained.
Lemma 1 g is strongly one-way on lengths in T .
Proof: Assume g is not strongly one-way on lengths in T . We proceed to derive a contradiction.
Since g is assumed not strongly one-way, there exists a p.p.t. algorithm B′ and a polynomial q(⋅) such
that for infinitely many m  T ,
T ,
![Pr[B ′ inverts g(U )] >--1--.
m q(m )](ln070x.png) | (1) |
Let M′ be the infinite set of integers for which inequality 1 holds, and let N′ = {n∣n2p(n)  M′}.
M′}.
We describe a p.p.t. algorithm A′ for inverting f on input y. First consider the procedure I′ for
inverting f.
| 1. Choose x1,…,xt(n)  {0,1}n uniformly and independently. {0,1}n uniformly and independently. |
| 2. Compute (z1,…,zt(n)) = B′(f(x1),…,f(xi-1),y,f(xi+1),…,f(xt(n))). |
| 3. If f(zi) = y, then halt and output zi and declare “success”. |
| If f(zi)≠y for all i, then halt and declare “failure”. |
Now, algorithm A′(y) runs I′(y) repeatedly a total of a(n) = 2n2 ⋅p(n) ⋅q(n2p(n)) times. If any of the runs of
I′(y) succeed, then A′ succeeds and gives the output of the first successful I′; otherwise, A′
fails.
For n  N′, we will show that
N′, we will show that
![P r[A′ inverts f (U )] > 1 --1-,
n p(n)](ln071x.png)
contradicting the assumption that f is weakly one-way.
Let
![n
Sn = {x | P r[I′ inverts f(x)] >--}
a(n )](ln072x.png)
be the set of good inputs of length n. Claim 1 shows that Sn is the set of inputs on which I′ succeeds
often enough so that A′ has an exponentially small failure probability.
Claim 1 For all x  Sn, Pr[A′ inverts f(x)] > 1 -
Sn, Pr[A′ inverts f(x)] > 1 -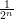 .
.
Proof: Immediate since for x  Sn,
Sn,
![( )
′ -n-- a(n) 1-- 1--
P r[A fails on f(x)] < 1- a(n) < en < 2n.](ln074x.png)
__
We now show in Claim 2 that almost all inputs x are in Sn for those lengths n that correspond to
values m = n2p(n)  M′ on which B′ has a success probability greater than 1∕q(m). (See inequality 1.)
M′ on which B′ has a success probability greater than 1∕q(m). (See inequality 1.)
Claim 2 For all n  N′,
N′,
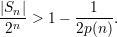
Proof: Assume to the contrary that
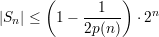 | (2) |
and let m = n2p(n). By inequality 1,
![s(n ) d=fP r[B ′ inverts g(Um )] >-1-.
q(m )](ln077x.png) | (3) |
The random variable Um consists of n ⋅ p(n) independent n-bit blocks Un(1),…,Un(n⋅p(n)).
Define
![s1(n) = P r[(B ′ inverts g(Um ))∧ (∃i)U(ni) ⁄∈ Sn];](ln078x.png)
![s2(n) = P r[(B ′ inverts g(Um ))∧ (∀i)U(ni) ∈ Sn].](ln079x.png)
Clearly, s(n) = s1(n) + s2(n).
We derive a contradiction by showing that both s1(n) and s2(n) are bounded from above by
n2 ⋅ p(n)∕a(n).
Note that
![P r[I′ inverts f (x )] ≥ Pr[B ′ inverts g(U ) | U (i)= x ]
m n](ln0710x.png) | (4) |
This is because algorithm I′ succeeds on y = f(x) whenever B′ succeeds on g(Um) and Un(i) = x.
Following the text, we have
Step (10) follows from inequality (4), and step (11) follows from the definition of Sn and the obvious fact
that Pr[I′ inverts f(x)] ≤ 1 since all events have probability at most 1.
The following bound on s2(n) holds for all sufficiently large n.
Here, step (12) follows from the definition of s2(n), step (13) is by the assumed inequality (2)), and
step (14) holds because every positive rational function is greater than an inverse exponential for all
sufficiently large n.
From (11) and (14), we have
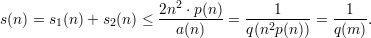
This contradicts (3), completing the proof of the claim. __
To finish the proof of the lemma, we observe that
![--1--
Pr[Un ∈ Sn] ≥ 1- 2p(n )](ln0714x.png)
follows immediately from claim 2, and
![1
P r[A ′ inverts f(Un ) | Un ∈ Sn ] ≥ 1--n
2](ln0715x.png)
follows from claim 1 since the bound applies to every x  Sn. Hence,
Sn. Hence,
This contradicts the assumption that f is weakly one-way with associated polynomial p(⋅), concluding the
proof of the lemma. __
 ℕ}. Let g be the function on length
n⋅t(n) strings defined by g(x1,…,xt(n)) = (f(x1),…,f(xt(n)), where |x1|,…,|xt(n)| = n. That is, given a
string x of length n ⋅ t(n), g splits it into t(n) length-n strings x1,…,xt(n), applies f(⋅) to each, and
concatenates the t(n) result strings so obtained.
ℕ}. Let g be the function on length
n⋅t(n) strings defined by g(x1,…,xt(n)) = (f(x1),…,f(xt(n)), where |x1|,…,|xt(n)| = n. That is, given a
string x of length n ⋅ t(n), g splits it into t(n) length-n strings x1,…,xt(n), applies f(⋅) to each, and
concatenates the t(n) result strings so obtained. ![Pr[B ′ inverts g(U )] >--1--.
m q(m )](ln070x.png)
![P r[A′ inverts f (U )] > 1 --1-,
n p(n)](ln071x.png)
![n
Sn = {x | P r[I′ inverts f(x)] >--}
a(n )](ln072x.png)
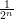
![( )
′ -n-- a(n) 1-- 1--
P r[A fails on f(x)] < 1- a(n) < en < 2n.](ln074x.png)
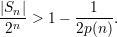
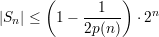
![s(n ) d=fP r[B ′ inverts g(Um )] >-1-.
q(m )](ln077x.png)
![s1(n) = P r[(B ′ inverts g(Um ))∧ (∃i)U(ni) ⁄∈ Sn];](ln078x.png)
![s2(n) = P r[(B ′ inverts g(Um ))∧ (∀i)U(ni) ∈ Sn].](ln079x.png)
![P r[I′ inverts f (x )] ≥ Pr[B ′ inverts g(U ) | U (i)= x ]
m n](ln0710x.png)
![s1(n) = P r[(∃i)((B′ inverts g(Um ))∧ U (ni)⁄∈ Sn )] (5)
n⋅p(n)
≤ ∑ P r[(B ′ inverts g(U ))∧ U (i)⁄∈ S ] (6)
m n n
i=1
n⋅∑p(n) ∑ ′ (i)
≤ Pr[(B inverts g(Um ))∧ U n = x] (7)
i=1 x⁄∈Sn
n⋅∑p(n) ∑
= Pr[U(ni)= x]⋅P r[B′ inverts g(Um ) | U(ni)= x] (8)
i=1 x⁄∈Sn
n⋅∑p(n) ′ (i)
≤ mxa⁄∈xSn{P r[B inverts g(Um ) | Un = x]} (9)
i=1
n⋅∑p(n)
≤ max {P r[I ′ inverts f(x)]} (10)
i=1 x⁄∈Sn
n n2 ⋅p(n)
≤ n ⋅p(n) ⋅---- = --------. (11)
a(n) a(n)](ln0711x.png)
![(i)
s2(n) ≤ P r[(∀i)Un ∈ Sn ] (12)
( 1 )n⋅p(n) 1
≤ 1- 2p(n) < -n∕2 (13)
2 2
< n-⋅p(n)- (14)
a(n )](ln0712x.png)
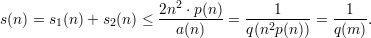
![--1--
Pr[Un ∈ Sn] ≥ 1- 2p(n )](ln0714x.png)
![1
P r[A ′ inverts f(Un ) | Un ∈ Sn ] ≥ 1--n
2](ln0715x.png)
![Pr[A′ inverts f (Un)] ≥ Pr[(A′ inverts f(Un))∧ Un ∈ Sn]
= Pr[Un ∈ Sn] ⋅Pr[A′ inverts f (Un) | Un ∈ Sn]
( ) ( )
≥ 1 - --1-- ⋅ 1- 1-- > 1 - --1-.
2p(n) 2n p(n)](ln0716x.png)