 T .
T .
 T , then there exists a valid proof y of x.
T , then there exists a valid proof y of x.YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Notes 16 (rev. 1) | |
| Professor M. J. Fischer | March 24, 2009 | |
Lecture Notes 16
Suppose Alice has encrypted all of her files and placed them on a public file server. She reveals one file to Bob by decrypting, perhaps because Alice runs a song library and Bob has paid her for that particular song. Bob doesn’t trust Alice and wants to know for sure that the song Alice just sent him is really the same one that is stored encrypted on the file server. How does Alice convince Bob that she sent him the right song?
One solution would be for Alice to send Bob the decryption key. Then Bob could decrypt the encrypted file himself. However, assuming all of the songs are encrypted using the same key, this would result in Bob learning the decryptions of all songs in the library. The question is whether there is some way for Alice to convince Bob that she gave him the correct song without giving him any other “knowledge” other than this one fact. A way of doing this, when it is possible, is called a zero-knowledge proof.
Here is another example. f is a one-way permutation, and b is a hard-core predicate for f. Alice has a secret x and makes y = f(x) public. She reveals the value of b(x) (a single bit 0 or 1). How can she convince Bob that the bit c she sent him is really the value of b(x) without also revealing additional information about x? Again, a zero-knowledge proof is desired.
Both of these problems are examples of situations in which Alice has secret information x which determines some value v = g(x) that she wants to give to Bob. She wants to convince Bob that v is correct without revealing any more information about x than is implied by the fact v = g(x).
To begin the discussion of zero knowledge proofs, we look first at the question of what it means to “convince” Bob of the truth of a statement such as v = g(x).
In classical mathematics, a convincing argument is called a proof. It is generally formalized as a sequence of logical statements such that each statement in the sequence is a self-evident truth called an axiom, or it follows from one or more previous statements using a valid rule of inference. All statements in the proof are considered to be valid, and the last statement is called the theorem that the proof establishes.
One generally assumes that there are feasible algorithms for testing if a given statement is an axiom and for testing if a statement follows from one or more previous statements using a valid rule of inference. Given such algorithms, one can then verify the validity of the statements in the proof one at a time in sequence, starting from the top. If all statements check out, then the last statement, which is the theorem to be proved, is also valid. Obviously, a proof system is only useful if the given algorithms are feasible.
Let T be the set of valid statements (theorems) that one wishes to prove. A proof system for T is a proof system that satisfies the following conditions:
 T .
T .
 T , then there exists a valid proof y of x.
T , then there exists a valid proof y of x.That is, anything provable is a valid theorem, and every valid theorem has a proof.
The above discussion focuses completely on the problem faced by the verifier of a proof – how does
one check that a proof is correct? But the proof comes from someone. We call the agent who
produces the proof the prover. We can then view this classical paradigm as a two-party protocol
between P (the prover) and V (the verifier). Given a statement x to be proven, P constructs
a proof y and sends it to V . V verifies that y is a valid proof and checks that the last line of
y is equal to x, the theorem to be proved. If so V accepts the proof y as a valid proof of x;
otherwise V rejects y. Assuming a sound and complete proof system for T , it follows that V
accepts only statements x  T , and for every x
T , and for every x  T , there is a prover that will cause V to accept
x.
T , there is a prover that will cause V to accept
x.
With classical proofs, we do not discuss the problem of how the prover comes up with a proof of x. In particular, we do not assume that P is a polynomial time algorithm (or even that it is an algorithm at all). All that matters is whether a proof of x exists or not.
We remark that proofs are only interesting for statements that the verifier can’t (efficiently) compute directly. For example, the veracity of the statement 1 + 2 = 3 is easily checked by just evaluating the left and right hand sides and checking for equality, so supplying a proof of that fact does not materially ease the verifier’s job.
On the other hand, let L be an 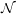
 language. Recall from section 3.5 that L
language. Recall from section 3.5 that L 
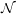
 iff there is a
polynomial-time computable relation RL(x,y) and a polynomial q(n) such that
iff there is a
polynomial-time computable relation RL(x,y) and a polynomial q(n) such that
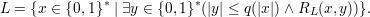
A string y is a witness to x’s membership in L iff |y|≤ q(|x|) and RL(x,y) is true.
Although there is no known feasible algorithm for deciding statements of the form x  L, with the help
of a witness y, it is easy to verify that x
L, with the help
of a witness y, it is easy to verify that x  L. Namely, just check (x,y)
L. Namely, just check (x,y)  RL. Thus, y can be considered to
be a “proof” of x, not in the classical sense described above, but in the sense of their being a feasible
verification algorithm (RL) for determining whether or not a string y is a valid proof of the statement
x
RL. Thus, y can be considered to
be a “proof” of x, not in the classical sense described above, but in the sense of their being a feasible
verification algorithm (RL) for determining whether or not a string y is a valid proof of the statement
x  L.
L.
Interactive proofs generalize the classical framework in several respects:
These vague requirements will be made more precise below.
We formalize the notion of two parties P and V interacting according to a protocol. Intuitively, P and V are concurrent algorithms that can send and receive messages. However, in order to simplify the reasoning, we assume that P and V are not truly concurrent but that they instead take turns: When it is P ’s turn, P runs until it is done with this phase and V waits. When P is done, the message it has constructed is transmitted to V , P is suspended, and V is activated. Now V runs until it is done with this phase, at which point it is suspended and P is reactivated with the message from V . This back-and-forth computation continues until one of the machines halts (rather than suspending), in which case the protocol stops. Note that it is possible for one of the machines to run forever during its phase, in which case the other machine remains suspended forever and never makes further progress.
We formalize the parties P and V as particular kinds of Turing machines. An interactive Turing machine M is a Turing machine with several tapes:
Let A and B be interactive Turing machines. A joint computation of A and B consists of placing a common input x on the input tapes of both A and B, placing an infinite sequence of independent uniformly distributed random bits on A’s and B’s random tapes, and placing 0 on the switch tape. (The switch tape determines which machine is currently activated – 0 for A and 1 for B.) Control switches from A to B when A writes 1 on the switch tape. At that time, the system copies the contents of A’s outgoing communication tape to B’s incoming communication tape, suspends A, and resumes B. Similarly, when B changes the switch tape from 1 to 0, the system suspends B, copies its outgoing communication tape to A’s incoming communication tape, and resumes A. This process continues until one of the machines halts, at which time the contents of the two output tapes is considered to be the result of the joint computation.1
For interactive proofs, we are generally only interested in the output of the verifier. We write ⟨A,B⟩(x) to denote the output of B in the joint computation of A and B with common input x.
Interactive Turing machine A has time complexity t : ℕ → ℕ if for all interactive Turing machines B, for all inputs x, and for all random tapes, A never takes more than t(|x|) steps.2 A is polynomial-time if there exists a polynomial p such that A has time complexity p.
Definition: An interactive proof system for a language L is a pair of interactive Turing machines (P,V ) such that V is polynomial-time and the following conditions are satisfied:
 L,
L, ![P r[⟨P, V⟩(x) = 1] ≥ 2.
3](ln161x.png)
 L and all interactive Turing machines B,
L and all interactive Turing machines B, ![Pr[⟨B,V ⟩(x) = 1] ≤ 1.
3](ln162x.png)
The class 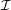
 consists of all languages having interactive proof systems
consists of all languages having interactive proof systems
Note that completeness depends on both P and V , whereas soundness is a property just of V .
Clearly, 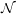
 ⊆
⊆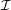
 since an interactive proof system can be easily constructed from the polynomial-time relation
RL described in section 39. Namely, if x
since an interactive proof system can be easily constructed from the polynomial-time relation
RL described in section 39. Namely, if x  L, P sends V a witness y to x
L, P sends V a witness y to x  L. V in turn checks that |y|≤ q(|x|) and
(x,y)
L. V in turn checks that |y|≤ q(|x|) and
(x,y)  RL.3
Note in particular that P is not required to be polynomial-time; only V is.
RL.3
Note in particular that P is not required to be polynomial-time; only V is.
Also, 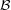

 ⊆
⊆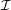
 . In this case, the prover need do nothing; the polynomial-time probabilistic Turing
machine M that recognizes L
. In this case, the prover need do nothing; the polynomial-time probabilistic Turing
machine M that recognizes L 
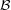

 can be used directly as the verifier, where output 1 means
“accept” and 0 means “reject”. Hence,
can be used directly as the verifier, where output 1 means
“accept” and 0 means “reject”. Hence, 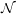
 ∪
∪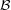

 ⊆
⊆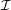
 . Recall that it is not known whether
. Recall that it is not known whether
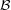

 ⊆
⊆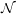
 .
.
As with the definition of 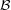

 , the error bounds of 2∕3 and 1∕3 in the definition can be varied
considerably without changing the concept being defined.
Definition: Let c,s : ℕ →
, the error bounds of 2∕3 and 1∕3 in the definition can be varied
considerably without changing the concept being defined.
Definition: Let c,s : ℕ → 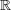 be functions satisfying c(n) - s(n) >
be functions satisfying c(n) - s(n) > 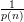 for some polynomial p(⋅). A
generalized interactive proof system for a language L with completeness bound c(⋅) and soundness bound
s(⋅) is a pair of interactive Turing machines (P,V ) such that V is polynomial-time and the following
conditions are satisfied:
for some polynomial p(⋅). A
generalized interactive proof system for a language L with completeness bound c(⋅) and soundness bound
s(⋅) is a pair of interactive Turing machines (P,V ) such that V is polynomial-time and the following
conditions are satisfied:
 L,
L, ![P r[⟨P, V⟩(x) = 1] ≥ c(|x|).](ln164x.png)
 L and all interactive Turing machines B,
L and all interactive Turing machines B, ![Pr[⟨B,V ⟩(x) = 1] ≤ s(|x|).](ln165x.png)
g(n) = c(n) - s(n) is called the acceptance gap and e(n) = max{1 - c(n),s(n)} is called the error probability.
By this definition, an interactive proof system (P,V ) is a generalized interactive proof system with completeness bound c(n) = 2∕3 and soundness bound s(n) = 1∕3. The acceptance gap and error probability are both 1/3.
We present the following non-trivial claim without proof.
Claim 1 The following three conditions on a language L are equivalent:

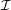
 .
.
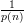 . Furthermore, the completeness bound c(n) and the soundness
bound s(n) for this system can be computed in time polynomial in n.
. Furthermore, the completeness bound c(n) and the soundness
bound s(n) for this system can be computed in time polynomial in n. This claim is useful in two ways. If we are given L 
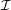
 , we can assume the existence of an interactive
proof system (P,V ) with exponentially small error bound (condition 2). On the other hand, if we
are tying to establish L
, we can assume the existence of an interactive
proof system (P,V ) with exponentially small error bound (condition 2). On the other hand, if we
are tying to establish L 
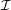
 , it suffices to construct an interactive proof system (P,V ) with
polynomial-time computable completeness and soundness bounds that have a non-negligible acceptance
gap.
, it suffices to construct an interactive proof system (P,V ) with
polynomial-time computable completeness and soundness bounds that have a non-negligible acceptance
gap.

The graph non-isomorphism language, GNI, is the set of all pairs of graphs (G1,G2) such that G1 is not
isomorphic4
to G2, written G1 ⁄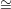 G2.
G2.
An interactive proof system for GNI is based on the following idea. The verifier picks one
of G1 or G2 at random and generates a random graph H isomorphic to it. Because 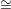 is a
transitive relation, if G1 ⁄
is a
transitive relation, if G1 ⁄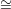 G2, then H is isomorphic to exactly one of G1 and G2 but not to
both. The prover determines which graph H is isomorphic to and returns the index of that
graph (1 or 2), which the verifier then checks. On the other hand, if G1
G2, then H is isomorphic to exactly one of G1 and G2 but not to
both. The prover determines which graph H is isomorphic to and returns the index of that
graph (1 or 2), which the verifier then checks. On the other hand, if G1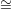 G2, the prover gets
no information about which graph was used to generate H since H is equally likely to result
whether starting from G1 or G2. Hence, the prover returns the correct index with probability at
most 1/2, so with probability 1/2 the verifier rejects. Repeating this protocol twice lowers the
error probability to below 1/3, as required by the definition of
G2, the prover gets
no information about which graph was used to generate H since H is equally likely to result
whether starting from G1 or G2. Hence, the prover returns the correct index with probability at
most 1/2, so with probability 1/2 the verifier rejects. Repeating this protocol twice lowers the
error probability to below 1/3, as required by the definition of 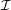
 . (Alternatively, one can
conclude directly from Claim 1 that GNI
. (Alternatively, one can
conclude directly from Claim 1 that GNI 
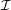
 since the acceptance gap of this protocol is
1∕2.)
since the acceptance gap of this protocol is
1∕2.)
We refer the reader to section 4.2.2 of the textbook for the detailed construction and proof.
However, we make special note of Claim 4.2.9.1, which formalizes the argument presented above
that the prover gets “no information” about the graph chosen by the verifier in the case that
G1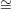 G2.
G2.
To give a few of the details, the verifier chooses a random value ξ  {1,2} and a random H = Π(Gξ),
where for each graph G, Π(G) is a uniformly distributed random variable over the set {G′∣G′
{1,2} and a random H = Π(Gξ),
where for each graph G, Π(G) is a uniformly distributed random variable over the set {G′∣G′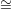 G}. We
must establish that the random variables ξ and H so defined are statistically independent, that is, for each
τ
G}. We
must establish that the random variables ξ and H so defined are statistically independent, that is, for each
τ  {1,2} and each graph G′
{1,2} and each graph G′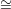 G1
G1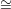 G2,
G2,
![P r[ξ = τ | H (G ) = G′] = P r[ξ = τ ] = 1.
ξ 2](ln1615x.png) | (1) |
This is what says the prover’s probability of correctly guessing ξ after receiving the graph H is still only 1∕2.
Our proof will make use of Bayes’ theorem, which relates the a priori probability of an event A to the a posteriori probability of A given that event B has occurred.
Theorem 1 (Bayes’ Theorem) Let A and B be events with non-zero probability. Then
![( Pr[A ])
P r[A | B] = Pr[B | A ]------
Pr[B ]](ln1616x.png)
![P r[A | B]=df P-r[A-∩-B-].
Pr[B ]](ln1617x.png) | (2) |
from which it follows that
![Pr[A | B ]⋅P r[B ] = P r[A ∩B ].](ln1618x.png) | (3) |
Using equation 3 twice (once with the roles of A and B reversed), we obtain
![Pr[A | B ]⋅P r[B ] = P r[A ∩ B ] = P r[B | A] ⋅Pr[A],](ln1619x.png)
from which the theorem easily follows. __
For a graph G′, the isomorphism class of G′ is the set [G′] = {G∣G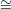 G′}. (This is the set of
all graphs isomorphic to G′.) Since
G′}. (This is the set of
all graphs isomorphic to G′.) Since 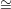 is an equivalence relation and G1
is an equivalence relation and G1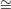 G2, we have that
[G1] = [G2]. Call that set S and let α = 1∕|S|. Let G′,G′′
G2, we have that
[G1] = [G2]. Call that set S and let α = 1∕|S|. Let G′,G′′ S. The random variable Π(G′′) is
uniformly distributed over S, so Pr[Π(G′′) = G′] = α, independent of the choice of G′ and
G′′.
S. The random variable Π(G′′) is
uniformly distributed over S, so Pr[Π(G′′) = G′] = α, independent of the choice of G′ and
G′′.
By the definition of conditional probability, we have
![′ ′
P r[Π (Gξ) = G | ξ = 1] = P r[Π(G1 ) = G ]
= α
= P r[Π(G ) = G ′]
2 ′
= P r[Π(G ξ) = G | ξ = 2].](ln1623x.png)
Applying Bayes’ theorem and the fact that Pr[ξ = 1] = Pr[ξ = 2] = 1∕2, we get
![( )
P r[ξ = 1 | Π (Gξ) = G′] = P r[Π (G ξ) = G′ | ξ = 1]⋅---P-r[ξ-=-1]---
P r[Π (Gξ) = G′]
′ ( P r[ξ = 2] )
= P r[Π (G ξ) = G | ξ = 2]⋅ P-r[Π-(G-)-=-G′]
′ ξ
= P r[ξ = 2 | Π(G ξ) = G ].](ln1624x.png)
![′ ′
Pr[ξ = 1 | Π (Gξ) = G ]+ P r[ξ = 2 | Π(G ξ) = G ] = 1,](ln1625x.png)
equation 1 follows.
We mention briefly another generalization of interactive proof systems that will be needed later. Namely, it is sometimes useful to permit an interactive Turing machine to have an additional private input tape. We write ⟨P(y),V (z)⟩(x) to denote V ’s output on a joint computation with common input x, private input y for P , and private input z for V . The time complexity is still measured in terms of the length of the common input x, so a machine with time complexity t must never use more than t(|x|) steps, regardless of its private input. In particular, such a machine might not be able to read all of its private input and still stay within the allowed time bound.
We extend the completeness and soundness conditions from section 40.3 to account for the additional inputs as follows:
 L, there exists y
L, there exists y  {0,1}* such that for all z
{0,1}* such that for all z  {0,1}*
{0,1}*
![2-
P r[⟨P (y ),V (z)⟩(x) = 1] ≥ 3.](ln1626x.png)
 L, for all interactive Turing machines B, and for all y,z
L, for all interactive Turing machines B, and for all y,z  {0,1}*,
{0,1}*,
![P r[⟨B (y ),V (z)⟩(x ) = 1] ≤ 1.
3](ln1627x.png)