![df
p(s,v) = P r[A (Cs(v)) = v].](ln200x.png)
YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| CPSC 461b: Foundations of Cryptography | Notes 20 (rev. 1) | |
| Professor M. J. Fischer | April 7, 2009 | |
Lecture Notes 20
In the last lecture, although the formal secrecy definition for bit-commitment is in terms indistinguishability, I was talking informally as if it were the same as unpredictability. This isn’t quite right, since the notion of indistinguishability does not depend on any assumed probability distribution on v, whereas a definition of secrecy based on unpredictability requires an assumed underlying distribution.
Recall that indistinguishability is introduced in section 26 of lecture notes 10. Unpredictability is introduced in the context pseudorandom generators in section 30 of lecture notes 12. I review these concepts in terms of bit-commitment.
Given a commitment scheme Cs(v), a predictor is a p.p.t. algorithm A that tries to guess v given Cs(v). It succeeds on a given run iff it outputs v. Since A itself is probabilistic, A has a success probability p(s,v) given by
![df
p(s,v) = P r[A (Cs(v)) = v].](ln200x.png)
Its overall success probability on v with security parameter n is p′n(v) = p(Un,v), that is, we average p(s,v) over all s of length n. Now, it is tempting to say that secrecy holds if p′n(V ) = 1∕2 + ϵ(n) for some negligible function ϵ(n), where V is a random variable ranging over {0,1}. This definition works if V is uniformly distributed. However, when V is not uniformly distributed, we may be able to correctly guess V with success probability significantly greater than 1∕2 based solely on knowledge of the distribution, and this ability to predict does not indicate a weakness in the commitment scheme. For example, if Pr[V = 1] = 2∕3, then the strategy of always guessing V = 1 is correct 2∕3 of the time, that is, p′n(V ) = 2∕3.
What we want instead is a definition based on the information about v that is provided by the commitment c = Cs(v). Namely, we’ll say that the commitment scheme satisfies secrecy if knowledge of c increases an adversary A’s success probability at correctly guessing v by only a negligible amount over what it could do without knowing c.
Formally, a bit-commitment scheme Cs(v) is unpredictable iff for all p.p.t. algorithms A and all distributions V over {0,1},
![Pr[A(CUn (V)) = V] ≤ max {Pr[V = 0],P r[V = 1]} + ϵ(n )](ln201x.png)
where ϵ(n) is a negligible function.
Coming back to indistinguishability, the general definition of secrecy given in section 48 of lecture notes 19, when applied to a simple one-way communication scheme Cs(v), just says that the probability ensembles
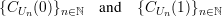
are computationally indistinguishable.
We invite the reader to think about how to show that an unpredictable bit-commitment scheme satisfies indistinguishability and vice versa.
The Goldwasser-Micali quadratic residue cryptosystem QR can be used for bit commitment. The idea is that any quadratic residue modulo n is a commitment to 0, and any quadratic non-residue with Jacobi symbol 1 is a commitment to 1.
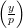 =
= 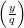 = -1. This implies that y has Jacobi symbol
= -1. This implies that y has Jacobi symbol 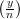 = 1
and that y is not a quadratic residue modulo n. (Note that these two facts hold even if p
and/or q are composite.) The sender then generates a random string x of length n, computes
c = (x2 mod n) if v = 0 and c = (x2y mod n) if v = 1, and sends c to the receiver. Thus, c
is a quadratic residue iff v = 0.
= 1
and that y is not a quadratic residue modulo n. (Note that these two facts hold even if p
and/or q are composite.) The sender then generates a random string x of length n, computes
c = (x2 mod n) if v = 0 and c = (x2y mod n) if v = 1, and sends c to the receiver. Thus, c
is a quadratic residue iff v = 0.
Secrecy is based on the (presumed) indistinguishability of random quadratic residues from random quadratic non-residues with Jacobi symbol 1. Unambiguity is perfect since a given number c either is or is not a quadratic residue modulo n.
Note that there is a subtle issue here when a probabilistic primality testing algorithm is used in finding
the primes p and q, for there is a non-zero probability that it will fail and result in numbers p and q that are
not prime. Nevertheless, y cannot be a quadratic residue modulo n since if it were, then we would have
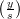 = 1 for every prime divisor s of n, but
= 1 for every prime divisor s of n, but 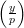 = -1 implies that
= -1 implies that 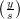 = -1 for some prime divisor s
of p.
= -1 for some prime divisor s
of p.
The commitment protocol needed for G3C is a little more general in two respects than what we have discussed so far.
As usual, to prove zero knowledge, we construct a simulator M* for V *’s view of its interaction with PG3C. Assume that q(n) is a polynomial that bounds V *’s running time. Here’s what M* does on input G = (V,E):
 {1,2,3}.
{1,2,3}.
 {0,1}n.
{0,1}n.
 {0,1}q(n) on its random coins tape, and
(d1,…,dn) on its incoming message tape.
{0,1}q(n) on its random coins tape, and
(d1,…,dn) on its incoming message tape.
Claim 1 Pr[M*(G) = ⊥] ≤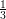 +
+ 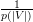 ≤
≤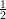 .
.
Proof: M*(G) outputs ⊥ iff V * chooses an edge (u,v), both of whose endpoints are colored the same. If the choice of edge were completely independent of the coloring, then the probability of the two endpoints being colored the same (assuming each vertex is colored uniformly and independently from {1,2,3}) would be exactly 1∕3. In fact, the choice of edge is not independent of the coloring since V * has access to the commitments of the coloring. We are thus led to analyze the probabilities in greater detail.
Let pu,v(G,r,(e1,…,en)) be the probability (over all choices for s1,…,sn) that V * on (G,r,(Cs1(e1),…,Csn(en))) replies with (u,v).
Subclaim Assume that Cs satisfies non-uniform secrecy. Then for every positive polynomial p(⋅),
every sufficiently large graph G = (V,E), every r  {0,1}q(n), every edge (u,v)
{0,1}q(n), every edge (u,v)  E, and every
two sequences α,β
E, and every
two sequences α,β  {1,2,3}n, it holds that
{1,2,3}n, it holds that
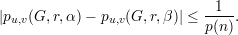
Proof: The proof of the subclaim is by a reducibility argument. Assuming the subclaim is false, we construct a distinguisher for the commitment scheme that violates non-uniform secrecy. (See textbook for details.) __
To finish the proof of the claim, one must calculate probabilities that (u,v) is chosen given

 {1,2,3}n by analyzing the number of illegally colored edges in each
{1,2,3}n by analyzing the number of illegally colored edges in each  . Again, we refer the reader to
the textbook for details. __
. Again, we refer the reader to
the textbook for details. __
Claim 2 For every probabilistic polynomial-time algorithm A, every positive polynomial p(⋅), and all sufficiently large graphs G = (V,E),
![* * PG3C ---1--
|P r[A (M (G)) = 1 | M (G ) ⁄= ⊥]- P r[A(viewV * (G )) = 1]| < p(|V |).](ln2015x.png)
We omit the rather complicated proof and refer the interested reader to the textbook.
Definition: Let L1, L2 be languages. L1 is polynomial-time reducible to L2, written L1 ≤p L2, if there exists a polynomial-time computable function f such that for all x,
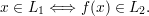
A language L′ is 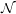
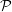 -complete if L ≤p L′ for every L
-complete if L ≤p L′ for every L 
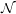
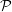 . It follows that if L′ could be
decided in polynomial time, then every language L
. It follows that if L′ could be
decided in polynomial time, then every language L 
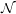
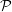 could be decided in polynomial time.
This would show that
could be decided in polynomial time.
This would show that 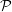 =
= 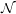
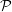 , settling one of the most important questions of computer
science.
, settling one of the most important questions of computer
science.
The language G3C is known to be 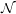
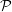 -complete, so for every L
-complete, so for every L 
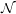
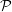 , there exists a
polynomial-time function fL such that L ≤p G3C via fL. In addition, there is a function gL that maps
witnesses for L to witnesses for G3C. Let RL be the defining polynomial-time relation for L. (See
section 3.5 of lecture notes 1.) Thus, if (x,w)
, there exists a
polynomial-time function fL such that L ≤p G3C via fL. In addition, there is a function gL that maps
witnesses for L to witnesses for G3C. Let RL be the defining polynomial-time relation for L. (See
section 3.5 of lecture notes 1.) Thus, if (x,w)  RL, then gL(x,w) is a 3-coloring of the graph
fL(x).
RL, then gL(x,w) is a 3-coloring of the graph
fL(x).

We now come to the main theorem of this unit.
Theorem 1 (4.4.11 of textbook) Suppose that there exists a commitment scheme satisfying the
(non-uniform) secrecy and unambiguity requirements. Then every language in 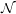
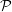 has an
auxiliary-input zero-knowledge proof system. Furthermore, the prescribed prover in this system can
be implemented in probabilistic polynomial time provided it gets the corresponding
has an
auxiliary-input zero-knowledge proof system. Furthermore, the prescribed prover in this system can
be implemented in probabilistic polynomial time provided it gets the corresponding 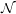
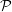 -witness as
auxiliary input.
-witness as
auxiliary input.
Proof: We describe the auxiliary-input interactive proof system for a language L. The common
input is a string x  L. The prover receives a witness w on its (private) auxiliary input. Both
parties compute G = fL(x). The prover computes ψ = gL(x,w), a 3-coloring of G. The prover
and verifier then jointly run as a subprotocol the auxiliary-input zero-knowledge interactive proof
system for G3C on common input G and prover’s auxiliary input ψ to prove that G
L. The prover receives a witness w on its (private) auxiliary input. Both
parties compute G = fL(x). The prover computes ψ = gL(x,w), a 3-coloring of G. The prover
and verifier then jointly run as a subprotocol the auxiliary-input zero-knowledge interactive proof
system for G3C on common input G and prover’s auxiliary input ψ to prove that G  G3C. V
accepts x
G3C. V
accepts x  L iff it accepts G
L iff it accepts G  G3C in the subprotocol. __
G3C in the subprotocol. __