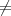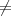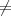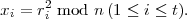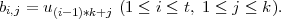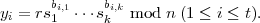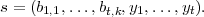YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 467a: Cryptography and Computer Security | Notes 19 (rev. 2) |
| Professor M. J. Fischer | | November 14, 2006 |
|
|
|
| |
93 Composing Zero-Knowledge Proofs
One round of the simplified FFS protocol has probability 0.5 of error. That is, Mallory could fool Bob half
the time. This is unacceptably high for most applications. By repeating the protocol t times, we reduce this
error probability to 1∕2t. Taking t = 20, for example, reduces the probability of error to less than on in a
million. The downside of such serial repetition is that it also requires t round trip messages between Alice
and Bob (plus a final message from Alice to Bob).
94 Parallel Execution of Zero-Knowledge Proofs
One could also imagine running the t executions of the protocol in parallel. Let (xi,bi,yi) be the messages
exchanged during the ith execution of the simplified FFS protocol, 1 ≤ i ≤ t. In a protocol execution, Alice
sends (x1,…,xt) to Bob, then Bob sends (b1,…,bt) to Alice, then Alice sends (y1,…,yt) to
Bob, and finally Bob checks the t sets of values he has received, accepting only if all checks
pass.
A parallel execution is certainly attractive in practice, for it reduces the number of round-trip
messages between Alice and Bob to only 1 1/2. The downside is that the resulting protocol
may not be zero knowledge by our definition. Intuitively, the important difference between the
serial and parallel versions of the protocol is that in the latter, Bob gets to know all of the xi’s
before choosing the bi’s. While it seems implausible that this would actually help a cheating
Bob to compromise Alice secret, the simulation proof used to show that a protocol is zero
knowledge no longer works. First Sam would have to guess (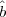 1,…
1,…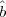 t). Then he can construct the xi’s
and yi’s as before. But when he finally gets to the point in Mallory’s program that Mallory
generates the bi’s, the chance is very high that his initial guesses were wrong and he will be
forced to start over again. Indeed, the probability that all t initial guesses are correct is only
1∕2t.
t). Then he can construct the xi’s
and yi’s as before. But when he finally gets to the point in Mallory’s program that Mallory
generates the bi’s, the chance is very high that his initial guesses were wrong and he will be
forced to start over again. Indeed, the probability that all t initial guesses are correct is only
1∕2t.
95 Full Feige-Fiat-Shamir Authentication Protocol
The full Feige-Fiat-Shamir Authentication Protocol combines ideas of serial and parallel execution to get a
protocol that exhibits some of the properties of both.
A Blum prime is a prime p such that p ≡ 3 (mod 4). A Blum integer is a number n = pq, were p and q
are both Blum primes. A special property of Blum integers is that if a is a quadratic residue modulo n, then
exactly one of a’s four square roots modulo n is itself a quadratic residue.
To see this, note that a is a quadratic residue modulo both p and q. Claim 3, section 64, of lecture
notes 12, shows that one of a’s two square roots is a quadratic residue modulo p, say bp. Then -bp is not a
quadratic residue since -1 is not a quadratic residue modulo the Blum prime p by the Euler Criterion of
lecture notes 12, section 63. Similar, exactly one of a’s two square roots modulo q is a quadratic residue.
Applying the Chinese Remainder Theorem, it follows that exactly one of a’s four square roots modulo n is
a quadratic residue.
To generate the public and private keys of the full FFS protocol, Alice chooses a Blum integer n. Next
she chooses random numbers s1,…,sk  Z*
n and random bits c1,…,ck
Z*
n and random bits c1,…,ck  {0,1}. From these, she computes
vi = (-1)cisi-2 mod n, for i = 1,…,k. She makes (n,v1,…,vk) public and keeps (n,s1,…,sk)
private.
{0,1}. From these, she computes
vi = (-1)cisi-2 mod n, for i = 1,…,k. She makes (n,v1,…,vk) public and keeps (n,s1,…,sk)
private.
Notice that every vi is either a quadratic residue or the negation of a quadratic residue. It is easily
shown that all of the vi have Jacobi symbol 1 modulo n. A round of the protocol itself is shown in
Figure 1. The protocol is repeated for a total of t rounds.
To see that the protocol works when both Alice and Bob are honest, one needs to verify that Bob’s
checks will succeed. Plugging in for y, we get that

Since vi = (-1)cisk-2, it follows that si2vi = (-1)ci. Hence,

Moreover, since x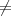 0, then also z
0, then also z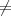 0. Hence, Bob’s checks succeed.
0. Hence, Bob’s checks succeed.
The chance that a bad Alice can fool Bob is only 1∕2kt. The authors recommend k = 5 and t = 4 for a
failure probability of 1∕220.
96 Non-interactive Interactive Proofs
We have seen that going from a serial composition of interactive proofs to a parallel version reduces
communication overhead but possibly at the sacrifice of zero knowledge. Rather surprisingly, one can go a
step further to eliminate the interaction from interactive proofs altogether.
The idea here is that Alice will provide Bob with a trace of an execution of herself in an interactive
protocol with Bob. Bob will check the trace to make sure that it is a possible record of an interaction
between the two of them when both are following the protocol. Of course, that isn’t enough to
convince Bob that Alice isn’t cheating, for how does he ensure that Alice simulates random
query bits bi for him, and how does he ensure that Alice chooses her xi’s before knowing the
bi’s?
The solution to both of these puzzles is to make the bi’s depend in an unpredictable way on the xi’s. We
do this by choosing the bi’s from the value of a hash function applied to the concatenation of the xi’s.
Here’s how it works in, say, the parallel composition of t copies of the simplified FFS protocol. The honest
Alice chooses x1,…,xt according to the protocol. Next she chooses b1…bt to be the first t bits of
H(x1 xt). Finally, she computes y1,…,yt, again according to the protocol. She sends Bob a single
message consisting of x1,…,xt,y1,…,yt. Bob computes b1…bt to be the first t bits of H(x1
xt). Finally, she computes y1,…,yt, again according to the protocol. She sends Bob a single
message consisting of x1,…,xt,y1,…,yt. Bob computes b1…bt to be the first t bits of H(x1 xt) and then
performs each of the t checks of the FFT protocol, accepting Alice’s proof only if all checks
succeed.
xt) and then
performs each of the t checks of the FFT protocol, accepting Alice’s proof only if all checks
succeed.
A cheating Alice can choose yi arbitrarily and then compute a valid xi for a given bi. But if she chooses
the bi’s first, the chance that the xi’s she then computes will hash to a string that begins with b1…bt is only
1∕2t.
If some bi does not agree with the corresponding bit of the hash function, she can either change bi and try
to find a new yi that works with the given xi, or she can change xi to try to get the ith bit of
the hash value to change. However, neither of these approaches works. The former requires
knowledge of Alice’s secret; the latter will cause all of the bits of the hash function to change
“randomly”.
Note that one way Alice can attempt to cheat is to use a brute-force attack. For example, she could
generate all of the xi’s to be squares of the yi with the hopes that the hash of the xi’s will make all bi = 0.
But that is likely to require 2t-1 attempts on average. If t is chosen large enough (say t = 80), the
number of trials Alice would have to do in order to have a significant probability of success is
prohibitive.
Of course, these observations are not a proof that Alice can’t cheat; only that the obvious strategies
don’t work. Nevertheless, it is plausible that a cheating Alice not knowing Alice’s secret, really wouldn’t be
able to find a valid such “non-interactive interactive proof”.
Even if this is so, there is an important difference between the true interactive proofs we have been
discussing and this kind of non-interactive proof. With a true zero-knowledge interactive proof, Bob does
not learn anything about Alice’s secret, nor can Bob impersonate Alice to Carol after Alice has
authenticated herself to Bob. On the other hand, if Alice sends Bob a valid non-interactive proof, then Bob
can in turn send it on to Carol. Even though Bob couldn’t have produced it on his own, it is still valid. So
here we have the curious situation that Alice needs her secret in order to produce the non-interactive proof
string π, and Bob can’t learn Alice’s secret from π, but now Bob can use π itself in an attempt to
impersonate Alice to Carol.
97 Feige-Fiat-Shamir Signatures
A signature scheme has a lot in common with the “non-interactive interactive” proofs introduced in
section 96. In both cases, there is only a one-way communication from Alice to Bob. Alice signs a message
and sends it to Bob. Bob then verifies it without further interaction with Alice. If Bob hands the message to
Carol, then Carol can also verify that it was signed by Alice.
Not surprisingly, the “non-interactive interactive proof” ideas can be used to turn the Feige-Fiat-Shamir
authentication protocol of section 95 into a signature scheme. The signature scheme we present here is
based on a slightly simplified version of the aforementioned protocol in which all of the vi’s in the public
key are quadratic residues, and n is not required to be a Blum integer, only a product of two distinct odd
primes. The public verification key is (n,v1,…,vk), and the private signing key is (n,s1,…,sk), where
vj = sj-2 mod n (1 ≤ j ≤ k).
To sign a message m, Alice simulates t rounds of the protocol in parallel. She first chooses random
r1,…,rt  Zn -{0} and computes
Zn -{0} and computes
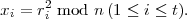
Next she computes u = H(mx1 xt), where H is a suitable cryptographic hash function. She chooses
b1,1,…,bt,k according to the first tk bits of u, that is,
xt), where H is a suitable cryptographic hash function. She chooses
b1,1,…,bt,k according to the first tk bits of u, that is,
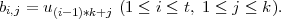
Finally, she computes
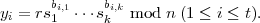
The signature is
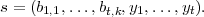
To verify the signed message (m,s), Bob computes
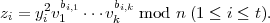
Bob checks that each zi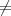 0 and that b1,1,…,bt,k are equal to the first tk bits of H(mz1
0 and that b1,1,…,bt,k are equal to the first tk bits of H(mz1 zt).
zt).
When both Alice and Bob are honest, it is easily verified that zi = xi (1 ≤ i ≤ t). In that case, Bob’s
checks all succeed since xi 0 and H(mz1
0 and H(mz1 zt) = H(mx1
zt) = H(mx1 xt).
xt).
To forge Alice’s signature, an impostor must find bi,j’s and yi’s that satisfy the equation
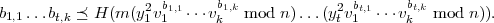
where “≼” means string prefix. It is not obvious how to solve such an equation without knowing a square
root of each of the vi-1’s and following essentially Alice’s procedure.
98 Two-Part Secret Splitting
There are many situations in which one wants to grant access to a resource only if a sufficiently
large group of agents cooperate. For example, a store safe might require both the manager’s
key and the armored car driver’s key in order to be opened. This protects the store against a
dishonest manager or armored car driver, and it also prevents an armed robber from coercing
the manager into opening the safe. A similar 2-key system is used for safe deposit boxes in
banks.
We might like to achieve the same properties for cryptographic keys or other secrets. For
example, if k is the secret decryption key for a cryptosystem, one might wish to split k into two
shares k1 and k2. By themselves, neither k1 nor k2 reveals any information about k, but when
suitably combined, k can be recovered. A simple way to do this is to choose k1 uniformly at
random and then let k2 = k ⊕ k1. Both k1 and k2 are uniformly distributed over the key space
and hence give no information about k. However, combined with XOR, they reveal k, since
k = k1 ⊕ k2.
Indeed, the one-time pad cryptosystem of lecture notes 3, section 14, can be viewed as an instance of
secret splitting. Here, Alice’s secret is her message m. The two shares are the ciphertext c
and the key k. Neither by themselves gives any information about m, but together they reveal
m = k ⊕ c.
99 Multi-Part Secret Splitting
Secret splitting generalizes to more than two shares. Imagine a large company that restricts access to
important company secrets to only its five top executives, say the president, vice-president,
treasurer, CEO, and CIO. They don’t want any executive to be able to access the data alone since
they are concerned that an executive might be blackmailed into giving confidential data to a
competitor. On the other hand, they also don’t want to require that all five executives get together to
access their data, both because this would be cumbersome and also because they worry about
the death or incapacitation of any single individual. They decide as a compromise that any
three of them should be able to access the secret data, but not one or two of them operating
alone.
A (τ,k) threshold secret splitting scheme splits a secret s into shares s1,…,sk. Any subset of τ or more
shares allows s to be recovered, but no subset of shares of size less than τ gives any information about
s.
 1,…
1,… t). Then he can construct the xi’s
and yi’s as before. But when he finally gets to the point in Mallory’s program that Mallory
generates the bi’s, the chance is very high that his initial guesses were wrong and he will be
forced to start over again. Indeed, the probability that all t initial guesses are correct is only
1∕2t.
t). Then he can construct the xi’s
and yi’s as before. But when he finally gets to the point in Mallory’s program that Mallory
generates the bi’s, the chance is very high that his initial guesses were wrong and he will be
forced to start over again. Indeed, the probability that all t initial guesses are correct is only
1∕2t.

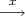
 .
.