YALE UNIVERSITY
DEPARTMENT OF COMPUTER SCIENCE
| | CPSC 467a: Cryptography and Computer Security | Notes 2 (rev. 3) |
| Professor M. J. Fischer | | September 8, 2008 |
|
|
|
| |
8 Compromising a cryptosystem
We’ve already mentioned one kind of compromise of a cryptosystem—learning the secret message m. But
actually there are many different degrees of compromise, some more serious than others, depending on the
application. Here is a list of some of the kinds of compromise which one should be aware of and ideally be
able to prevent:
-
Complete break
- Eve finds the key k. Eve now has the same knowledge as both Alice and Bob, so
she can impersonate Alice when talking to Bob and impersonate Bob when talking to Alice.
She can also passively read all communications between Alice and Bob.
-
Complete message recovery
- Eve can recover any message m even without knowing k. She can
thus passively read all communications between Alice and Bob, but she can’t impersonate
one to the other since she is unable to produce encrypted messages herself.
-
Selected message recovery
- Eve is only able to recover certain messages from their ciphertexts.
Namely, there is a set M ⊆
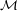 of messages which Eve is able to read; others remain secure.
The larger the set M is, the more serious this kind of compromise.
of messages which Eve is able to read; others remain secure.
The larger the set M is, the more serious this kind of compromise.
-
Uncertain message recovery
- Eve is able to recover m from c only when certain keys k
 K ⊆
K ⊆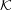 are in use. The larger the set K is, the more serious this kind of compromise. Because
the key is generally chosen randomly and uniformly from
are in use. The larger the set K is, the more serious this kind of compromise. Because
the key is generally chosen randomly and uniformly from 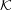 , Eve has probably |K|∕|
, Eve has probably |K|∕|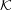 | of
compromising Alice’s messages.
| of
compromising Alice’s messages.
-
Partial message recovery
- In each of the above kinds of compromise, Eve either succeeds or
not in recovering m. In partial message recovery, she obtains partial information about m.
Initially, Eve knows only the probability distribution from which m is drawn. After seeing
the ciphertext c = Ek(m), Eve may be able to determine that m lies in a subset M ⊆
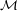 . If
|M| = 1, then Eve has narrowed down the possibilities for m to a single message, so she has
learned m. But if |M|≥ 2, she has obtained only partial information about M. Whether or
not that partial information is useful to Eve depends on what partial information she receives
and of course on the application.
. If
|M| = 1, then Eve has narrowed down the possibilities for m to a single message, so she has
learned m. But if |M|≥ 2, she has obtained only partial information about M. Whether or
not that partial information is useful to Eve depends on what partial information she receives
and of course on the application.
-
Perfect secrecy (information-theoretic security)
- This is the other extreme in which Eve learns
nothing at all about m from seeing the ciphertext c. Whatever she knew about m before seeing
c she still knows, but she learns nothing new from seeing c. (Note that if Eve already knew m
beforehand, then she would learn nothing new about m from seeing c, so in that special case,
all cryptosystems are totally secure.)
9 Probabilistic model
When we start talking about the probability of Even learning the message, we must ask, “Where does
randomness enter into the discussion of attacks on a cryptosystem?” We assume there are three such
places:
- The message itself is drawn at random from some probability distribution over the
message space
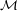 . That distribution is not necessarily uniform or even anything close to
uniform .
However, whatever the distribution is, we assume that it is part of Eve’s a priori knowledge.
. That distribution is not necessarily uniform or even anything close to
uniform .
However, whatever the distribution is, we assume that it is part of Eve’s a priori knowledge.
- The secret key is chosen uniformly from the key space
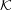 .
.
- The attacker (Eve) has access to a source of randomness which she may use while attempting
to break the system. For example, Eve can choose an element k′

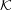 at random. With
probability p = 1∕|
at random. With
probability p = 1∕|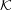 |, her element k′ is actually the correct key k.
|, her element k′ is actually the correct key k.
We further assume that these three sources of randomness are statistically independent. This means that
Eve’s random numbers do not depend on (nor give any information about) the message or key used
by Alice. It also means that Alice’s key does not depend on the particular message or vice
versa.
These multiple sources of randomness give rise to a joint probability distribution that assigns a
well-defined probability (i.e., a real number in the interval [0,1]) to each triple (m,k,z), where m is a
message, k a key, and z is the result of the random choices Eve makes during her computation. The
independence requirement simply says that the probability of the triple (m,k,z) is precisely the product of
pm ×pk ×pz, where pm is the probability that m is the chosen message, pk is the probability that k is the
chosen key, and pz is the probability that z represents the random choices made by Eve during the course of
her computation.
When talking about random choices, we often use the term random variable to denote the experiment
of choosing an element from a set according to a particular probability distribution. For example, we
sometimes use m to denote the random variable that describes the experiment of Alice choosing a message
m 
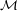 according to the assumed message distribution. Ambiguously, we often use m to denote a
particular element in the set
according to the assumed message distribution. Ambiguously, we often use m to denote a
particular element in the set 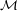 , perhaps the outcome of the experiment described by the random variable
m. While these two uses may sometimes be confusing, we will try to make which usage is intended clear
from context.
, perhaps the outcome of the experiment described by the random variable
m. While these two uses may sometimes be confusing, we will try to make which usage is intended clear
from context.
For example, if we let pm denote the probability that the message distribution assigns to the particular
message m 
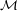 , then there is no experiment under consideration and it is clear that m is being used to
denote an element of
, then there is no experiment under consideration and it is clear that m is being used to
denote an element of 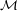 . On the other hand, if we talk about the event m = m0, then we are using m in the
sense of a random variable, and the event m = m0 means that the outcome of the experiment described by
m is m0. We denote the probability of that event occurring by prob[m = m0], which in this case
is simply pm0. See section 2.2 of Stinson for a more thorough review of basic probability
definitions.
. On the other hand, if we talk about the event m = m0, then we are using m in the
sense of a random variable, and the event m = m0 means that the outcome of the experiment described by
m is m0. We denote the probability of that event occurring by prob[m = m0], which in this case
is simply pm0. See section 2.2 of Stinson for a more thorough review of basic probability
definitions.
10 Perfect secrecy
Perfect secrecy is defined formally in terms of statistical independence. In our probabilistic model, we can
consider both m and k to be random variables. Together, they induce a probability distribution on the
ciphertext c = E(k,m). Here we see the power of the random variable notation, for c itself can be
considered to be a random variable which is a function of k and m. To define c formally, we must define the
probability of the events c = c0 for each c0 
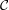 . These are easily derived from the random variables k and
m as follows:
. These are easily derived from the random variables k and
m as follows:
![∑
prob[c = c0] = prob[k = k0 ∧ m = m0 ].
k0,m0:c0=E (k0,m0)](ln020x.png)
Because of the assumed independence of k and m, this is the same as
![∑
prob[c = c0] = prob[k = k0]× prob[m = m0].
k0,m0:c0=E (k0,m0)](ln021x.png)
The reason for the summation is that the same ciphertext c0 can arise from many different key-message
pairs.
Now, what it means for the cryptosystem to have perfect secrecy (be information-theoretically secure)
is that the random variables c and m are statistically independent, that is,
![prob[m = m0 ∧ c = c0] = prob[m = m0 ]× prob[c = c0]](ln022x.png)
for all m0 
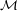 and c0
and c0 
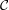 .
.
This independence is often expressed more intuitively in terms of conditional probabilities. We
define
![prob[m = m | c = c ] = prob[m-=-m0-∧c-=-c0]
0 0 prob[c = c0]](ln023x.png)
assuming the denominator of the fraction is non-zero. This is the probability that m = m0 given that
c = c0. We then say that c and m are statistically independent if
![prob[m = m0 | c = c0] = prob[m = m0 ]](ln024x.png)
for all m0 
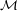 and c0
and c0 
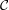 such that prob[c = c0]≠0. Hence, even after Eve receives the ciphertext c0, her
opinion of the likelihood of each message m0 is the same as it was initially, so she has learned nothing
about m0.
such that prob[c = c0]≠0. Hence, even after Eve receives the ciphertext c0, her
opinion of the likelihood of each message m0 is the same as it was initially, so she has learned nothing
about m0.
11 Caesar cipher
To make these ideas more concrete, we look at the Caesar cipher, which is said to go back to Roman times.
It is an alphabetic cipher, that is, used to encode the 26 letters of the Roman alphabet A,B,…,Z. For
convenience, we will represent the letters by the numbers 0,1,…,25, where A = 0, B = 1, …,
Z = 25.
11.1 Encrypting single letters
The base cipher handles just single letters. The message space is 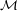 = {0,…,25}, and the ciphertext space
and key space are the same, so
= {0,…,25}, and the ciphertext space
and key space are the same, so 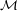 =
= 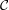 =
= 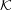 .
.
To encrypt, Ek replaces each letter m by the letter k places further on in the alphabet when read
circularly, with A following Z. To decrypt, Dk replaces each letter c by the letter k places earlier in the
alphabet when read circularly. Mathematically, the encryption and decryption functions are given
by
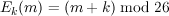
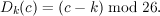
(Notation: x mod 26 is the remainder of x divided by 26.) Thus, if k = 3, then Ek(P) = S and
Dk(S) = P .
11.2 Encrypting strings
Of course, one is generally interested in encrypting more than single letter messages, so we need a way to
extend the encryption and decryption functions to strings of letters. The simplest way of extending is to
encrypt each letter separately using the same key k. If m1…mr is an r-letter message, then its encryption is
c1…cr, where ci = Ek(mi) = (mi + k) mod 26 for each i = 1,…,r. Decryption works similarly, letter by
letter.
What we have really done by the above is to build a new cryptosystem from the base cryptosystem on
single letters. In the new system, the message space and ciphertext space are
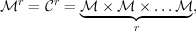
that is, length-r sequences of numbers from {0,…,25}. The encryption and decryption functions
are
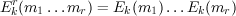
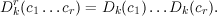
Here, we use the superscript r to distinguish these functions from the base functions Ek() and
Dk().
12 Probabilistic analysis of a simplified Caesar cipher
To make the ideas from Section 11 concrete, we work through a probabilistic analysis of a
simplified version of the Caesar cipher restricted to a 3-letter alphabet, so 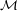 =
= 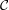 =
= 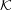 = {0,1,2},
Ek(m) = (m + k) mod 3, and Dk(m) = (m - k) mod 3.
= {0,1,2},
Ek(m) = (m + k) mod 3, and Dk(m) = (m - k) mod 3.
Assume for starters that the message distribution is given in Figure 12.1.
Because the keys are always chosen uniformly, each key has probability 1/3. Hence, we obtain the joint
probability distribution shown in Figure 12.2.
Next, we calculate the conditional probability distribution prob[m = 1∣c = 2]. To do this, we consider
the pairs (m,k) in our joint sample space and compute c = Ek(m) for each. Figure 12.3 shows the result,
where each point is labeled by a triple (m,k,c), and those points for which c = 2 are shown in
bold.
The probability that c = 2 is the sum of the probabilities that correspond to the bold face
points, i.e., prob[c = 2] = 1∕6 + 1∕9 + 1∕18 = 6∕18 = 1∕3. The only one of these points for
which m = 1 is (1,1,2), and it’s probability is 1∕9, so prob[m = 1 ∧ c = 2] = 1∕9. Hence,
This is the same as the initial probability that m = 1. Repeating this computation for each possible message
m0 and ciphertext c0, one concludes that
![prob[m = m0 | c = c0] = prob[m = m0 ].](ln0214x.png)
Hence, our simplified Caesar cipher is information-theoretically secure.
Now let’s make a minor change in the cipher and see what happens. The only change is that we reduce
the key space to 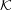 = {0,1}. The a priori message distribution is still given by Figure 12.1, but
the joint probability distribution changes as does the sample space as shown in Figure 12.4.
= {0,1}. The a priori message distribution is still given by Figure 12.1, but
the joint probability distribution changes as does the sample space as shown in Figure 12.4.
Now, prob[c = 2] = 1∕6 + 1∕12 = 3∕12 = 1∕4, and prob[m = 1 ∧ c = 2] = 1∕6. Hence,
![1∕6 2
prob[m = 1 | c = 2] =---= --.
1∕4 3](ln0216x.png)
While the a priori probability that m = 1 is still the same as it was before—1/3, the conditional probability
given c = 2 is now double what it was. Indeed, there are now only two possibilities for m once
Eve sees c = 2. Either m = 1 (and k = 1) or m = 2 (and k = 0). It is no longer possible
that m = 0 given that c = 2. Hence, Eve narrows the possibilities for m to the set {1,2}, and
her probabilistic knowledge of m changes from the initial distribution (1∕2,1∕3,1∕6) to the
new distribution (2∕3,1∕3). She has learned at lot about m indeed, even without finding it
exactly!
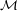 of messages which Eve is able to read; others remain secure.
The larger the set M is, the more serious this kind of compromise.
of messages which Eve is able to read; others remain secure.
The larger the set M is, the more serious this kind of compromise.
 K ⊆
K ⊆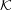 are in use. The larger the set K is, the more serious this kind of compromise. Because
the key is generally chosen randomly and uniformly from
are in use. The larger the set K is, the more serious this kind of compromise. Because
the key is generally chosen randomly and uniformly from 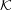 , Eve has probably |K|∕|
, Eve has probably |K|∕|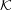 | of
compromising Alice’s messages.
| of
compromising Alice’s messages.
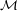 . If
|M| = 1, then Eve has narrowed down the possibilities for m to a single message, so she has
learned m. But if |M|≥ 2, she has obtained only partial information about M. Whether or
not that partial information is useful to Eve depends on what partial information she receives
and of course on the application.
. If
|M| = 1, then Eve has narrowed down the possibilities for m to a single message, so she has
learned m. But if |M|≥ 2, she has obtained only partial information about M. Whether or
not that partial information is useful to Eve depends on what partial information she receives
and of course on the application.
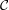
![∑
prob[c = c0] = prob[k = k0 ∧ m = m0 ].
k0,m0:c0=E (k0,m0)](ln020x.png)
![∑
prob[c = c0] = prob[k = k0]× prob[m = m0].
k0,m0:c0=E (k0,m0)](ln021x.png)
![prob[m = m0 ∧ c = c0] = prob[m = m0 ]× prob[c = c0]](ln022x.png)
![prob[m = m | c = c ] = prob[m-=-m0-∧c-=-c0]
0 0 prob[c = c0]](ln023x.png)
![prob[m = m0 | c = c0] = prob[m = m0 ]](ln024x.png)
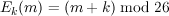
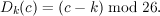
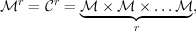
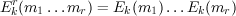
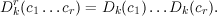
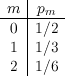
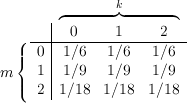

![prob[m = 1 | c = 2] = prob[m-=--1∧-c =-2]
prob[c = 2]
1 ∕9 1
= 1-∕3 = 3.](ln0213x.png)
![prob[m = m0 | c = c0] = prob[m = m0 ].](ln0214x.png)
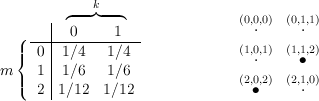
![1∕6 2
prob[m = 1 | c = 2] =---= --.
1∕4 3](ln0216x.png)