Part A. Written problems

Problem 1: Zero divisors

An element a Z_n -{0} is said to be a zero divisor modulo n if ab ≡ 0 (mod n) for some b Z_n -{0}.

1. Explain why there are no zero divisors in Z_p when p is prime.
2. Find a zero divisor in Z₃₉.
3. What is the value of the first element to repeat in the sequence

4. Do you think it is possible to find a non-zero number x Z₃₉ and a number k ≥ 0 such that x^k ≡ 0 (mod 39)? Why or why not? Would your answer change for some RSA modulus n other than 39?
5. Suppose n is not required to be an RSA modulus. Can you find numbers n,x,k such that x ⁄≡ 0 but x^k ≡ 0 (mod n)?

In all cases, justify your answers.

Problem 2: Greatest common divisor

The definition of greatest common divisor can be extended naturally to a sequence of numbers (a₁,a₂,…,a_k), not all of which are zero; namely, it is the largest integer d ≥ 1 such that d∣a_j for all j = 1,2,…,k. Describe an efficient algorithm for computing gcd(a₁,…,a_k), and explain why it computes the correct answer.

Problem 3: Euler’s totient function

Compute ϕ(2200). Show your work.

Problem 4: Euler theorem

Compute 3⁵⁹¹²⁰⁷ mod 2200.

Problem 5: Extended Euclidean algorithm

Use the extended Euclidean algorithm to solve the Diaphantine equation

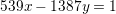
Show the resulting table of triples as in slide 34 of lecture 8 notes.
[Note: You may write a program to produce the table if you wish, but these numbers are small enough to make it quite feasible to carry out the computation by hand or with the aid of a pocket calculator.]

Part B. Programming problem

Problem 6: Factoring the RSA modulus knowing the public and private keys

Bob’s public RSA key is n = 1501, e = 323. Eve manages to learn that his decryption key is d = 539. Implement the randomized factoring algorithm shown on slide 49 of lecture 9 notes. Use your program to factor n. Once you have the factorization of n, compute ϕ(n), and check your answer by verifying that ed ≡ 1 (mod ϕ(n)).